题目内容
函数y=x+ (x≠0)的值域是________.
(x≠0)的值域是________.
(-∞,-4]∪[4,+∞)
分析:由于y′=1- =
=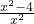 =
= ,利用y′>0,可求其单调递增区间,y′<0,可求其单调递减区间,从而可求其值域.
,利用y′>0,可求其单调递增区间,y′<0,可求其单调递减区间,从而可求其值域.
解答:解;∵由y′=1- =
=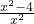 =
= =0得:x=2或x=-2,
=0得:x=2或x=-2,
∴当x>2或x<2时,y′>0,即函数y=x+ (x≠0)在(-∞,-2),(2,+∞)上单调递增;
(x≠0)在(-∞,-2),(2,+∞)上单调递增;
当-2<x<0或0<x<2时,y′<0,即函数y=x+ (x≠0)在(-2,0),(0,2)上单调递减;
(x≠0)在(-2,0),(0,2)上单调递减;
∴当x<0时,f(x)极大值=f(-2)=-4,
当x>0时,f(x)极小值=f(2)=4,
∴函数y=x+ (x≠0)的值域是(-∞,-4]∪[4,+∞).
(x≠0)的值域是(-∞,-4]∪[4,+∞).
故答案为:(-∞,-4]∪[4,+∞).
点评:本题考查函数的值域,通过求导讨论该函数的单调性与极值是解题的关键,也是难点所在,当然,也可以用基本不等式解决,属于中档题.
分析:由于y′=1-
 =
=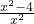 =
= ,利用y′>0,可求其单调递增区间,y′<0,可求其单调递减区间,从而可求其值域.
,利用y′>0,可求其单调递增区间,y′<0,可求其单调递减区间,从而可求其值域.解答:解;∵由y′=1-
 =
=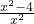 =
= =0得:x=2或x=-2,
=0得:x=2或x=-2,∴当x>2或x<2时,y′>0,即函数y=x+
 (x≠0)在(-∞,-2),(2,+∞)上单调递增;
(x≠0)在(-∞,-2),(2,+∞)上单调递增;当-2<x<0或0<x<2时,y′<0,即函数y=x+
 (x≠0)在(-2,0),(0,2)上单调递减;
(x≠0)在(-2,0),(0,2)上单调递减;∴当x<0时,f(x)极大值=f(-2)=-4,
当x>0时,f(x)极小值=f(2)=4,
∴函数y=x+
 (x≠0)的值域是(-∞,-4]∪[4,+∞).
(x≠0)的值域是(-∞,-4]∪[4,+∞).故答案为:(-∞,-4]∪[4,+∞).
点评:本题考查函数的值域,通过求导讨论该函数的单调性与极值是解题的关键,也是难点所在,当然,也可以用基本不等式解决,属于中档题.

练习册系列答案
相关题目