题目内容
(2006•广州一模)某射击运动员射击1次,击中目标的概率为
.他连续射击5次,且每次射击是否击中目标相互之间没有影响.
(Ⅰ)求在这5次射击中,恰好击中目标2次的概率;
(Ⅱ)求在这5次射击中,至少击中目标2次的概率.
| 4 | 5 |
(Ⅰ)求在这5次射击中,恰好击中目标2次的概率;
(Ⅱ)求在这5次射击中,至少击中目标2次的概率.
分析:(Ⅰ)设此人在这5次射击中击中目标的次数为ξ,则ξ~B(5,
),故在这5次射击中,恰好击中目标2次的概率为P5(2)=
•(
)2•(
)3,运算求出结果.
(Ⅱ)在这5次射击中,至少击中目标2次的概率等于1减去击中0次的概率,再减去只击中一次的概率.
| 4 |
| 5 |
| C | 5 2 |
| 4 |
| 5 |
| 1 |
| 5 |
(Ⅱ)在这5次射击中,至少击中目标2次的概率等于1减去击中0次的概率,再减去只击中一次的概率.
解答:解:(Ⅰ)设此人在这5次射击中击中目标的次数为ξ,则ξ~B(5,
),因此,有在这5次射击中,恰好击中目标2次的概率为P5(2)=
•(
)2•(
)3=
.
(Ⅱ)在这5次射击中,至少击中目标2次的概率等于1减去击中0次的概率,再减去只击中一次的概率,
故所求的概率为 P=1-P5(0)-P5(1)=1-
•(
)5-
•
•(
)4=
.
| 4 |
| 5 |
| C | 2 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 32 |
| 625 |
(Ⅱ)在这5次射击中,至少击中目标2次的概率等于1减去击中0次的概率,再减去只击中一次的概率,
故所求的概率为 P=1-P5(0)-P5(1)=1-
| C | 0 5 |
| 1 |
| 5 |
| C | 1 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 3104 |
| 3125 |
点评:本题主要考查二项分布、对立事件的概率,n次独立重复实验中恰好发生k次的概率,所求的事件的概率等于用1减去它的对立事件概率,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
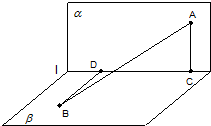 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,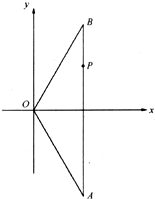 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.