题目内容
已知函数
，若对任意的x∈R，都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值为 ．
【答案】分析：由题意可以判断f（x1）是函数的最小值，f（x2）是函数的最大值，则|x1-x2|的最小值为相邻最值之间的横坐标的距离，就是半周期，求解即可．
解答：解：函数
，若对任意的x∈R，都有f（x1）≤f（x）≤f（x2），
所以f（x1）是函数的最小值，f（x2）是函数的最大值，则|x1-x2|的最小值为相邻最值之间的横坐标的距离，就是半周期，
因为T=
=4π，所以|x1-x2|的最小值为：2π．
故答案为：2π．
点评：本题是基础题，考查三角函数的周期的求法，准确理解题意，f（x1）是函数的最小值，f（x2）是函数的最大值，以及|x1-x2|的最小值的含义是解题的关键，考查计算能力．
解答：解：函数
，若对任意的x∈R，都有f（x1）≤f（x）≤f（x2），所以f（x1）是函数的最小值，f（x2）是函数的最大值，则|x1-x2|的最小值为相邻最值之间的横坐标的距离，就是半周期，
因为T=
=4π，所以|x1-x2|的最小值为：2π．故答案为：2π．
点评：本题是基础题，考查三角函数的周期的求法，准确理解题意，f（x1）是函数的最小值，f（x2）是函数的最大值，以及|x1-x2|的最小值的含义是解题的关键，考查计算能力．
练习册系列答案
相关题目
，若对任意的实数
，不等式
恒成立，则实数
的取值范围是
．
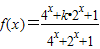．若对任意的实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，则实数k的取值范围是 ．
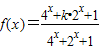．若对任意的实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，则实数k的取值范围是 ．