Question

已知函数f(x)＝lg(x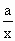＋－2)，其中a是大于零的常数．

(1)求函数f(x)的定义域．

(2)当a∈(1，4)时，求函数f(x)在[2，＋∞)上的最小值．

(3)若对任意x∈[2，＋∞)恒有f(x)＞0，试确定a的取值范围．

Answer 1

答案：
解析：

解：(1)由x＋－2＞0得＞0(*)，方程x2－2x＋a＝0的根的判别式Δ＝4(1－a)，当a＞1时，Δ＜0，x2－2x＋a＞0恒成立，则由(*)知x＞0；当0＜a≤1时，Δ≥0，x2－2x＋a＝[x－(1－)]·[x－(1＋)]， 　　(*)为＞0，；当0＜a≤1时，f(x)的定义域为(0，1－)∪(1＋，＋∞)；当a＞1时，f(x)的定义域为(0，＋∞)． 　　(2)当1＜a＜4时令g(x)＝x＋，设2≤x1＜x2，则g(x1)－g(x2)＝(x1＋)－(x2＋)＝(x1－x2)(1－)． 　　因为2≤x1＜x2，所以x1x2＞4．即＜．因为1＜a＜4，所以＜1．所以1－＞0．所以(x1－x2)(1－)＜0，所以g(x1)＜g(x2)，所以g(x)在[2，＋∞)为增函数．所以f(x)在[2，＋∞)为增函数．所以f(x)min＝f(2)＝lg． 　　(3)解法一： 　　①若0＜a≤1，则当x＝2时，f(2)＝lg(2＋－2)＝lg＜0不满足题设条件． 　　当1＜a＜4，由(2)知亦使对任意x∈[2，＋∞)恒有f(x)＞0只要f(2)＞0即lg＞0，a＞2，所以2＜a＜4． 　　②当a≥4时，f(x)＝lg(x＋－2)≥lg(2－2)＝lg(2－2)． 　　当x＝即x＝≥2时，[f(x)]min＝lg(2－2)≥lg2＞0，所以a≥4时满足对任意x∈[2，＋∞)恒有f(x)＞0．综上所述，当a＞2时对任意x∈[2，＋∞)恒有f(x)＞0． 　　解法二： 　　因为f(x)＝lg(x＋－2)＞0，所以x＋－2＞1．所以a＞3x－x2，x∈[2，＋∞)恒成立．而y＝3x－x2，x∈[2，＋∞)为减函数．所以它的最大值为2．所以a＞2．