题目内容
求证:1+2x4≥2x3+x2.
思路分析:根据所证不等式的两边均为多项式的特点,作差之后转化为完全平方式的形式,便于判断符号.故宜选用作差比较法.
证明:[方法一]
∵(1+2x4)-(2x3+x2)=2x3(x-1)-(x+1)(x-1)=(x-1)(2x3-x-1)
=(x-1)(2x3-2x+x-1)=(x-1)2(2x2+2x+1)=(x-1)2[2(x+![]() )2+
)2+![]() ]≥0,
]≥0,
∴1+2x4≥2x3+x2.
[方法二]
∵(1+2x4)-(2x3+x2)
=x4-2x3+x2+x4-2x2+1
=(x2-x)2+(x2-1)2≥0,
∴1+2x4≥2x3+x2.
方法归纳
证法一的变形主要是因式分解,其难点在于分解2x3-x-1的因式,判断2x2+2x+1的符号.除用配方法外,还可用判别式法;证法二的变形主要是配方法,难点在于拆项.通过本例可以了解作差比较法的全貌,以及关键的第二步变形.

练习册系列答案
相关题目
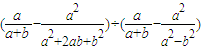 ;
;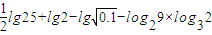 ;
;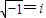 ,验算i是否方程2x4+3x3-3x2+3x-5=0的解;
,验算i是否方程2x4+3x3-3x2+3x-5=0的解;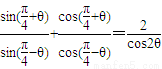 .
.