题目内容
如下图,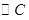 经过原点且与两坐标轴分别交于点A与点B,点A的坐标为
经过原点且与两坐标轴分别交于点A与点B,点A的坐标为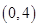 ,M是圆上一点,
,M是圆上一点,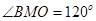 ,则圆心C的坐标
,则圆心C的坐标 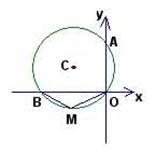
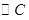 经过原点且与两坐标轴分别交于点A与点B,点A的坐标为
经过原点且与两坐标轴分别交于点A与点B,点A的坐标为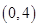 ,M是圆上一点,
,M是圆上一点, ,则圆心C的坐标
,则圆心C的坐标 
( )
)
 )
)连接BC、OC,过点C作CN⊥OB于N,CE⊥OA于E,根据已知条件,易证四边形CNOE是矩形,已知点A的坐标,易求OE=2,所以CN=2,已知∠BMO=120°,易求∠NCO=60°,所以NO=2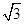 ,故点C的坐标可求.
,故点C的坐标可求.
解答:解:连接BC、OC,过点C作CN⊥OB于N,CE⊥OA于E,
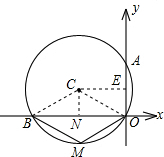
∵CN、CE过圆心,CN⊥BO,CE⊥AO,
∴AE=OE,ON=BN,
∴∠CNO=∠NOE=∠OEC=90°,
∴四边形CNOE是矩形(有三个角是直角的四边形是矩形),
∴CN=OE,
∵点A的坐标为(0,4),
∴OA=4,
∴OE=CN=2,
∵∠BMO=120°,
∴优弧BAO的度数为240°,
∴∠BCO=120°,
∴∠NCO=60°,
∴CE=NO=2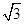 ,
,
∴C(-2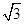 ,2).
,2).
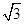 ,故点C的坐标可求.
,故点C的坐标可求.解答:解:连接BC、OC,过点C作CN⊥OB于N,CE⊥OA于E,

∵CN、CE过圆心,CN⊥BO,CE⊥AO,
∴AE=OE,ON=BN,
∴∠CNO=∠NOE=∠OEC=90°,
∴四边形CNOE是矩形(有三个角是直角的四边形是矩形),
∴CN=OE,
∵点A的坐标为(0,4),
∴OA=4,
∴OE=CN=2,
∵∠BMO=120°,
∴优弧BAO的度数为240°,
∴∠BCO=120°,
∴∠NCO=60°,
∴CE=NO=2
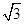 ,
,∴C(-2
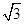 ,2).
,2).
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
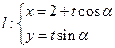 (
(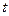 为参数),圆
为参数),圆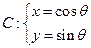 (
(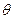 为参数).
为参数).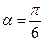 时,试判断直线
时,试判断直线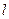 与圆
与圆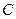 的位置关系;
的位置关系; 作直线
作直线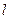 与圆
与圆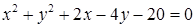 交于M、N两点,若
交于M、N两点,若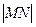 =8,则
=8,则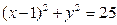 的弦AB的中点为P (2,—1),则直线AB的方程是____________________
的弦AB的中点为P (2,—1),则直线AB的方程是____________________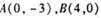 ,若点P是圆
,若点P是圆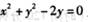 上的动点,则
上的动点,则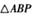 面积的最小值为
面积的最小值为