题目内容
设命题p:函数y=lg(x2+2x-c)的定义域为R.命题q:函数y=lg(x2+2x-c)的值域为R,若命题p、q有且仅有一个正确,则c的取值范围为( )A.![]() B.(-∞,-1) C.[-1,+∞] D.R
B.(-∞,-1) C.[-1,+∞] D.R
D
解析:本题考查函数定义域、值域求法.若命题p成立,即x2+2x-c>0恒成立,所以△<0,解之得c<-1;若命题q成立,即u(x)=x2+2x-c的值域为(0,+∞),所以△≥0,解之得c≥-1.当命题p成立q不成立时可解得c<-1,当命题q成立p不成立时可解得c≥-1,综上,c∈R.

练习册系列答案
相关题目
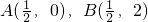 及直线
及直线 的距离相等,那么满足条件的点P有且只有1个.
的距离相等,那么满足条件的点P有且只有1个.