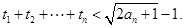题目内容
设函数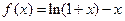 在区间
在区间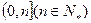 上的最小值为
上的最小值为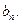 令
令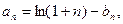
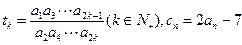 .
.
(Ⅰ)求 ;
;
(Ⅱ)试求所有的正整数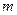 ,使得
,使得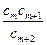 为数列
为数列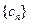 中的项;
中的项;
(Ⅲ)求证: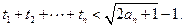
 ,
,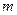 为
为
解析(Ⅰ)显然函数的定义域为
 ,
,
故函数 在区间
在区间 上是减函数
上是减函数
(Ⅱ)

 ,设
,设 ,
,
则 ,
,
所以 为8的约数
为8的约数 为奇数,
为奇数, 的取值可为
的取值可为
当 时,
时, 是数列
是数列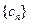 中的项
中的项
当 时,
时, ,而数列
,而数列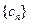 中的最小项为
中的最小项为 ,所以不符合
,所以不符合
故满足条件的所有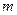 为
为
(Ⅲ)



又




练习册系列答案
相关题目
 .
. 的奇偶性;
的奇偶性; 上的最小值为
上的最小值为 ,求
,求 ,证明:方程
,证明:方程 有两个不同的正数解.
有两个不同的正数解. 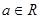 ,函数
,函数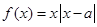 ,
,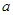 =2时,写出函数
=2时,写出函数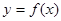 的单调递增区间;
的单调递增区间;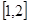 上的最小值;
上的最小值;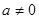 ,函数
,函数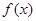 在
在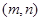 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出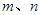 的取值范围(用
的取值范围(用 函数
函数 在区间
在区间 上的最大值与最小值之差
上的最大值与最小值之差 , 则
, 则 等于( )
等于( )  B.
3 C.
B.
3 C.  D.
9
D.
9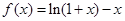 在区间
在区间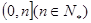 上的最小值为
上的最小值为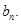 令
令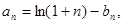
 .
.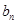 ;
;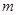 ,使得
,使得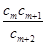 为数列
为数列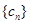 中的项;
中的项;