题目内容
(本小题满分12分)
对于函数 :
:
(Ⅰ) 是否存在实数 使函数
使函数 为奇函数?
为奇函数?
(Ⅱ) 探究函数 的单调性(不用证明),并求出函数
的单调性(不用证明),并求出函数 的值域.
的值域.
【答案】
解:(Ⅰ)(解法一)假设存在实数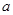 函数
函数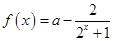 是奇函数,因为
是奇函数,因为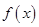 的定义域为
的定义域为 ,
,
所以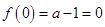 ,所以
,所以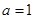 ……………2分
……………2分
此时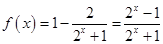 ,则
,则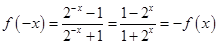 ,所以
,所以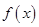 为奇函数
为奇函数
即存在实数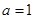 使函数
使函数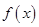 为奇函数.……………5分
为奇函数.……………5分
(解法二)假设存在实数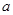 使函数
使函数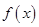 为奇函数,即有
为奇函数,即有
即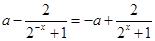 ,……………2分
,……………2分
所以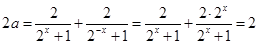
所以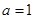 ,即存在实数
,即存在实数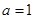 使函数
使函数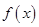 为奇函数.……………5分
为奇函数.……………5分
(Ⅱ)由(Ⅰ)知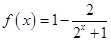 ,因为
,因为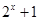 在
在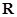 上递增,所以
上递增,所以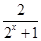 在
在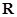 上递减,所以
上递减,所以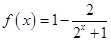 在
在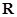 上递增.…………………8分
上递增.…………………8分
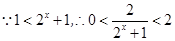 ,
,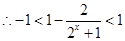 ,
,
即函数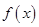 的值域为
的值域为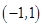 .……………12分
.……………12分
【解析】略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目