题目内容
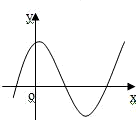
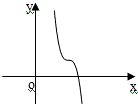
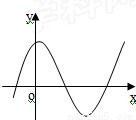
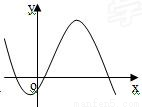
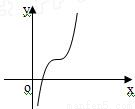
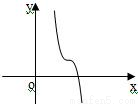
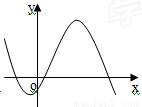
如下图，已知f（x）=ax3+bx2+cx+d（d≠0），记△=4（b2-3ac），则当△≤0，a＞0时，f（x）的大致图象为（ ）A．
B．
C．
D．
【答案】分析：求出f（x）的导函数，利用二次函数的判别式与二次函数图象的关系得到f′（x）≥0，得到函数是增函数．
解答：解：f′（x）=3ax2+2bx+c
其判别式为△=4（b2-3ac），
∵△≤0，a＞0
∴f′（x）≥0
∴f（x）为定义域上的增函数
∴f（x）的图象呈上升趋势
故选C
点评：本题考查二次函数的图象与判别式的关系、考查导函数大于0函数单增；导函数小于0函数单减．
解答：解：f′（x）=3ax2+2bx+c
其判别式为△=4（b2-3ac），
∵△≤0，a＞0
∴f′（x）≥0
∴f（x）为定义域上的增函数
∴f（x）的图象呈上升趋势
故选C
点评：本题考查二次函数的图象与判别式的关系、考查导函数大于0函数单增；导函数小于0函数单减．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知f（x）是定义在（-3，3）上的偶函数，当0＜x＜3时，f（x）的图象如下图所示，那么不等式f（x）sinx＜0的解集是（ ）
