题目内容
(文)在正方体ABCD—A1B1C1D1中,E是棱BB1中点,G是DD1中点,F是BC上一点且FB=A.30° B.120° C.60° D.90°
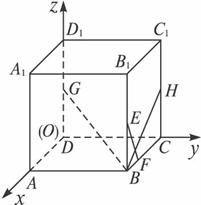
答案: (文)D 方法一:以D为坐标原点建立空间直角坐标系,如图,设棱长为4,则G(0,0,2),B(4,4,0),E(4,4,2),F(3,4,0).
∴![]() =(4,4,-2),
=(4,4,-2),![]() =(-1,0,-2),cos〈
=(-1,0,-2),cos〈![]() 〉=
〉=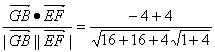 =0.
=0.
∴BG与EF所成的角为90°.
方法二:可用三垂线定理,取CC1的中点H,则BA为BG在面BCC1B1上的射影,
∵BH⊥EF,∴BG与EF所成角为90°.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目