Question

已知函数y=f（x）是R上的偶函数，且x≥0时，f（x）=（

1

2

）^x-1．
（1）求f（x）的解析式；
（2）画出此函数的图象．

Answer 1

分析：（1）可先设x＜0，则由已知可得f（-x）=（

1

2

）^-x-1，结合函数为偶函数可求
（2）结合指数函数的图象及函数的图象的平移可作出函数的图象

解答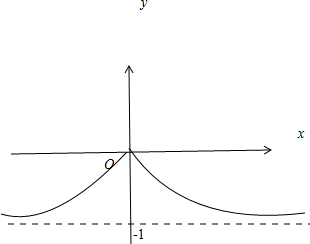：解：（1）当x＜0时，-x＞0
∴f（-x）=（

1

2

）^-x-1，
∵函数y=f（x）是偶函数
∴f（x）=f（-x）=（

1

2

）^-x-1=2^x-1
故f（x）=

( 1 2 )x-1，x≥0 2x-1，x＜0

（2）函数的图象如图所示

点评：本题主要考查了利用偶函数的性质求解函数的解析式，及知数函数的图象的作法，函数图象变换的应用．