题目内容
已知函数f(x)= (a>0,a≠1),记函数[f(x)-
(a>0,a≠1),记函数[f(x)- ][f(-x)-
][f(-x)- ]的值域为D,若元素t∈D,且t∈Z,则t的个数为
]的值域为D,若元素t∈D,且t∈Z,则t的个数为
- A.1个
- B.2个
- C.3个
- D.无穷多个
A
分析:由已知中f(x)= ,可得到函数[f(x)-
,可得到函数[f(x)- ][f(-x)-
][f(-x)- ]的解析式,结合指数函数的图象和性质,可求出D,进而得到满足条件的t的个数.
]的解析式,结合指数函数的图象和性质,可求出D,进而得到满足条件的t的个数.
解答:∵函数f(x)= =1-
=1-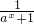
∴f(-x)= =
=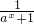
故f(x)+f(-x)=1
∴[f(x)- ][f(-x)-
][f(-x)- ]=[f(x)-
]=[f(x)- ][1-f(x)-
][1-f(x)- ]
]
=-[f(x)- ]2
]2
=-( -
-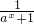 )2,
)2,
∵ax>0,故0<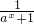 <1
<1
故
 -
-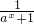

故 <-(
<-( -
-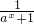 )2≤0
)2≤0
即D=( ,0]
,0]
由元素t∈D,且t∈Z,
故满足t的个数为1个
故选A
点评:本题考查的知识点是函数的值域,指数函数的图象和性质,其中根据书籍求出函数[f(x)- ][f(-x)-
][f(-x)- ]的解析式是解答的关键.
]的解析式是解答的关键.
分析:由已知中f(x)=
 ,可得到函数[f(x)-
,可得到函数[f(x)- ][f(-x)-
][f(-x)- ]的解析式,结合指数函数的图象和性质,可求出D,进而得到满足条件的t的个数.
]的解析式,结合指数函数的图象和性质,可求出D,进而得到满足条件的t的个数.解答:∵函数f(x)=
 =1-
=1-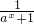
∴f(-x)=
 =
=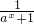
故f(x)+f(-x)=1
∴[f(x)-
 ][f(-x)-
][f(-x)- ]=[f(x)-
]=[f(x)- ][1-f(x)-
][1-f(x)- ]
]=-[f(x)-
 ]2
]2=-(
 -
-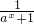 )2,
)2,∵ax>0,故0<
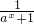 <1
<1故

 -
-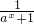

故
 <-(
<-( -
-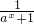 )2≤0
)2≤0即D=(
 ,0]
,0]由元素t∈D,且t∈Z,
故满足t的个数为1个
故选A
点评:本题考查的知识点是函数的值域,指数函数的图象和性质,其中根据书籍求出函数[f(x)-
 ][f(-x)-
][f(-x)- ]的解析式是解答的关键.
]的解析式是解答的关键. 
练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|