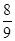题目内容
在面积为9的正方形ABCD内部随机取一点P,则能使△PAB的面积大于 的概率是________.
的概率是________.

分析:根据题意,得正方形边长为3,P到AB的距离为1,作出E、F为AD、BC的三等份点,由△PAB的面积大于
 ,分析可得符合条件的P在矩形CDEF内,易得矩形CDEF的面积,由几何概型公式计算可得答案.
,分析可得符合条件的P在矩形CDEF内,易得矩形CDEF的面积,由几何概型公式计算可得答案.解答:
 解:如图,正方形边长为3,P到AB的距离为1,
解:如图,正方形边长为3,P到AB的距离为1,作出E、F为AD、BC的三等份点,如图;
若△PAB的面积大于
 ,即符合条件的P在矩形CDEF内,
,即符合条件的P在矩形CDEF内,易得矩形CDEF的面积为6,
则△PAB的面积大于
 的概率为
的概率为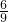 =
= ;
;故答案为:
 .
.点评:本题考查几何概型的运用,解题的关键在于分析得到P具有的性质,进而得到P所在的范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面四个命题:
①函数y= 在(2,
在(2, )处的切线与直线2x-y+1=0垂直;
)处的切线与直线2x-y+1=0垂直;
②已知a= (sint+cost)dt,则(x-
(sint+cost)dt,则(x- )6展开式中的常数项为
)6展开式中的常数项为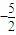 ,
,
③在边长为1的正方形ABCD内(包括边界)有一点M,则△AMB的面积大于或等于 的概率为
的概率为
④在一个2×2列联表中,由计算得K2=13,079,则其两个变量有关系的可能性是99.9%.
其中所有正确的命题序号是 .
①函数y=
 在(2,
在(2, )处的切线与直线2x-y+1=0垂直;
)处的切线与直线2x-y+1=0垂直;②已知a=
 (sint+cost)dt,则(x-
(sint+cost)dt,则(x- )6展开式中的常数项为
)6展开式中的常数项为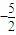 ,
,③在边长为1的正方形ABCD内(包括边界)有一点M,则△AMB的面积大于或等于
 的概率为
的概率为
④在一个2×2列联表中,由计算得K2=13,079,则其两个变量有关系的可能性是99.9%.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 内部随机取一点
内部随机取一点 ,则能使
,则能使 的面积大于3的概率是( )
的面积大于3的概率是( ) B.
B. C.
C. D.
D.