题目内容
“0＜a≤1”是“关于x的方程ax2+2x+1=0至少有一个负根”的（ ）
分析：这是一个二次型方程，首先我们要分析当a=0时，方程是否有负根，再分析当a≠0时，方程存在负根的情况，综合即可得到结论．
解答：解：当a=0时，方程ax2+2x+1=0
可化为方程2x+1=0方程存在一个负根
当a≠0时，若关于x的二次方程ax2+2x+1=0有根
则△=4-4a≥0，即a≤1
若方程ax2+2x+1=0无负根
则x1+x2=-
≥0，x1•x2=
≥0，
这种情况不存在
故关于x的方程ax2+2x+1=0，至少有一个负根的充要条件是a≤1
又“0＜a≤1”成立，“a≤1”但反之“a≤1”成立，“0＜a≤1”不一定成立，
所以“0＜a≤1”是“关于x的方程ax2+2x+1=0至少有一个负根”的充分不必要条件．
故选A．
可化为方程2x+1=0方程存在一个负根
当a≠0时，若关于x的二次方程ax2+2x+1=0有根
则△=4-4a≥0，即a≤1
若方程ax2+2x+1=0无负根
则x1+x2=-
| 2 |
| a |
| 1 |
| a |
这种情况不存在
故关于x的方程ax2+2x+1=0，至少有一个负根的充要条件是a≤1
又“0＜a≤1”成立，“a≤1”但反之“a≤1”成立，“0＜a≤1”不一定成立，
所以“0＜a≤1”是“关于x的方程ax2+2x+1=0至少有一个负根”的充分不必要条件．
故选A．
点评：本题考查的知识点是一元二次方程的根的分布与系数的关系，充要条件的判断，其中容易忽略当a=0时的情况．
练习册系列答案
相关题目
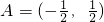，B=（-1，1，2，3），设S是B的含有两个“元”的子数组，求C（A，S）的最大值；
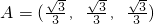，B=（0，a，b，c），且a2+b2+c2=1，S为B的含有三个“元”的子数组，求C（A，S）的最大值．
，B=（-1，1，2，3），设S是B的含有两个“元”的子数组，求C（A，S）的最大值；
，B=（0，a，b，c），且a2+b2+c2=1，S为B的含有三个“元”的子数组，求C（A，S）的最大值．
，B=（-1，1，2，3），设S是B的含有两个“元”的子数组，求C（A，S）的最大值；
，B=（0，a，b，c），且a2+b2+c2=1，S为B的含有三个“元”的子数组，求C（A，S）的最大值；
．设数组Bm（m=1，2，3，…，n）含有四个“元”bm1，bm2，bm3，bm4，且
，求A与Bm的所有含有三个“元”的子数组的关系数C（A，Bm）（m=1，2，3，…，n）的最大值．