题目内容

已知二次函数f(x)=x2-2(10-3n)x+9n2-61n+100(n∈N*),设函数y=f(x)图象的顶点到x轴的距离构成数列{an},到y轴的距离构成数列{bn}.

(1)求数列{an}的前n项和Sn,数列{bn}的前n项和Tn.

(2)试比较Sn与Tn的大小.

解：(1)f(x)=x2-2(10-3n)x+9n2-61n+100

    =［x-(10-3n)］2-n.

    ∴顶点(10-3n,-n).

    依题意an=n,bn=|10-3n|,

    ∴Sn=.

    Tn=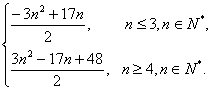

    (2)当n≤3时,Tn-Sn==-2n2+8n＞0.

    ∴Sn＜Tn.

    当n≥4时,Tn-Sn==n2-9n+24=(n-3)2+15＞0.

    ∴Sn＜Tn.

    综上,Sn＜Tn.

练习册系列答案
相关题目
已知二次函数f(x)=ax2+bx+
1
2
满足f（1+x）=f（1-x）且方程f(x)=
5
2
-x有等根
（1）求f（x）的表达式；
（2）若f（x）在定义域（-1，t]上的值域为（-1，1]，求t的取值范围；
（3）是否存在实数m、n（m＜n），使f（x）定义域和值域分别为[m，n]和[2m，2n]，若存在，求出m、n的值．
已知二次函数f(x)=ax2+bx+c，函数y=f(x)+
2
3
x-1的图象过原点且关于y轴对称，记函数 h(x)=
x
f(x)．
（I）求b，c的值；
（Ⅱ）当a=
1
10
时，求函数y=h(x)的单调递减区间；
（Ⅲ）试讨论函数 y=h（x）的图象上垂直于y轴的切线的存在情况．
已知二次函数f(x)=ax2+bx+1和g(x)=
bx-1a2x+2b

（1）f（x）为偶函数，试判断g（x）的奇偶性；
（2）若方程g（x）=x有两个不相等的实根，当a＞0时判断f（x）在（-1，1）上的单调性；
（3）若方程g（x）=x的两实根为x1，x2f（x）=0的两根为x3，x4，求使x3＜x1＜x2＜x4成立的a的取值范围．
已知二次函数f(x)=
-x2-x+2
的定义域为A，若对任意的x∈A，不等式x2-4x+k≥0成立，则实数k的最小值为
3
3
．
已知二次函数f(x)=ax2+bx+1和g(x)=
bx-1a2x+2b

（1）f（x）为偶函数，试判断g（x）的奇偶性；
（2）若方程g（x）=x有两个不相等的实根，当a＞0时判断f（x）在（-1，1）上的单调性；
（3）当b=2a时，问是否存在x的值，使满足-1≤a≤1且a≠0的任意实数a，不等式f（x）＜4恒成立？并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网