题目内容
已知函数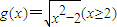 的导数为
的导数为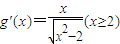 ,记函数f(x)=x-kg(x)(x≥2,k为常数).
,记函数f(x)=x-kg(x)(x≥2,k为常数).(1)若函数f(x)在区间(2,+∞)上为减函数,求k的取值范围;
(2)求函数f(x)的值域.
【答案】分析:(1)根据函数f(x)在区间(2,+∞)上为减函数可得到f(x1)-f(x2)关于x1,x2的关系式,然后转化为 对x1,x2∈(2,+∞)恒成立的问题,即可得到k的取值.
对x1,x2∈(2,+∞)恒成立的问题,即可得到k的取值.
(2)对函数f(x)进行求导,然后分两种情况讨论,当k≤0时易知函数f(x)是增函数,可直接求出值域;当k>0时,又分三种情况k>1、k=1、0<k<1根据导数的正负情况进行讨论,从而可得到函数的单调性确定值域.
解答:解:(1)因为f(x)在区间(2,+∞)上为减函数,
所以对任意的x1,x2∈(2,+∞),且x1<x2恒有f(x1)-f(x2)>0成立.
即 恒成立.
恒成立.
因为x2-x1>0,所以 对x1,x2∈(2,+∞),且x1<x2时,恒成立.
对x1,x2∈(2,+∞),且x1<x2时,恒成立.
又 <1,所以k≥1.
<1,所以k≥1.
(2) .
.
下面分两种情况讨论:
(1)当k≤0时, 是关于x的增函数,值域为
是关于x的增函数,值域为
(2)当k>0时,又分三种情况:
①当k>1时,因为 ,所以
,所以 ,即f'(x)<0.
,即f'(x)<0.
所以f(x)是减函数, .
.
又 ,
,
当x→+∞,f(x)→-∞,所以f(x)值域为 .
.
②当k=1时, ,
,
且f(x)是减函数,故f(x)值域是 .
.
③当0<k<1时,f'(x)是增函数,
 ,
, .
.
下面再分两种情况:
(a)当 时,f'(x)=0的唯一实根
时,f'(x)=0的唯一实根 ,
,
故f'(x)>0(x≥2), 是关于x的增函数,值域为
是关于x的增函数,值域为 ;
;
(b)当 时,f'(x)=0的唯一实根
时,f'(x)=0的唯一实根 ,
,
当 时,f'(x)<0;当
时,f'(x)<0;当 时,f'(x)>0;
时,f'(x)>0;
所以f(x) .故f(x)的值域为
.故f(x)的值域为 .
.
综上所述,f(x)的值域为 ;
;
 (
( );
); (k=1);
(k=1); (k>1).
(k>1).
点评:本题主要考查函数的单调性与其导函数的正负之间的关系、根据导数求函数的值域.导数是高考必考点,要重视.
 对x1,x2∈(2,+∞)恒成立的问题,即可得到k的取值.
对x1,x2∈(2,+∞)恒成立的问题,即可得到k的取值.(2)对函数f(x)进行求导,然后分两种情况讨论,当k≤0时易知函数f(x)是增函数,可直接求出值域;当k>0时,又分三种情况k>1、k=1、0<k<1根据导数的正负情况进行讨论,从而可得到函数的单调性确定值域.
解答:解:(1)因为f(x)在区间(2,+∞)上为减函数,
所以对任意的x1,x2∈(2,+∞),且x1<x2恒有f(x1)-f(x2)>0成立.
即
 恒成立.
恒成立.因为x2-x1>0,所以
 对x1,x2∈(2,+∞),且x1<x2时,恒成立.
对x1,x2∈(2,+∞),且x1<x2时,恒成立.又
 <1,所以k≥1.
<1,所以k≥1.(2)
 .
.下面分两种情况讨论:
(1)当k≤0时,
 是关于x的增函数,值域为
是关于x的增函数,值域为
(2)当k>0时,又分三种情况:
①当k>1时,因为
 ,所以
,所以 ,即f'(x)<0.
,即f'(x)<0.所以f(x)是减函数,
 .
.又
 ,
,当x→+∞,f(x)→-∞,所以f(x)值域为
 .
.②当k=1时,
 ,
,且f(x)是减函数,故f(x)值域是
 .
.③当0<k<1时,f'(x)是增函数,
 ,
, .
.下面再分两种情况:
(a)当
 时,f'(x)=0的唯一实根
时,f'(x)=0的唯一实根 ,
,故f'(x)>0(x≥2),
 是关于x的增函数,值域为
是关于x的增函数,值域为 ;
;(b)当
 时,f'(x)=0的唯一实根
时,f'(x)=0的唯一实根 ,
,当
 时,f'(x)<0;当
时,f'(x)<0;当 时,f'(x)>0;
时,f'(x)>0;所以f(x)
 .故f(x)的值域为
.故f(x)的值域为 .
.综上所述,f(x)的值域为
 ;
; (
( );
); (k=1);
(k=1); (k>1).
(k>1).点评:本题主要考查函数的单调性与其导函数的正负之间的关系、根据导数求函数的值域.导数是高考必考点,要重视.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目