题目内容
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴的垂线交C于点N.
(1)写出抛物线的焦点坐标及准线方程;
(2)证明:抛物线C在点N处的切线与直线AB平行;
(3)是否存在实数k使
•
=0,若存在,求k的值;若不存在,说明理由.
(1)写出抛物线的焦点坐标及准线方程;
(2)证明:抛物线C在点N处的切线与直线AB平行;
(3)是否存在实数k使
| NA |
| NB |
分析:(1)抛物线方程化为标准方程,即可写出抛物线的焦点坐标及准线方程;
(2)求出N点的坐标,可得切线方程,代入抛物线方程,利用线l与抛物线C相切,可得结论;
(3)假设存在,利用数量积公式及韦达定理计算即可得出结论.
(2)求出N点的坐标,可得切线方程,代入抛物线方程,利用线l与抛物线C相切,可得结论;
(3)假设存在,利用数量积公式及韦达定理计算即可得出结论.
解答: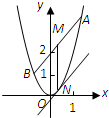 (1)解:将y=2x2化为x2=
(1)解:将y=2x2化为x2=
y,则焦点坐标是(0,
),准线方程是y=-
…2分
(2)证明:如图,设A(x1,2x12),B(x2,2x22),把y=kx+2代入y=2x2得2x2-kx-2=0,
由韦达定理得x1+x2=
,x1x2=-1,.…4分
∴xN=xM=
=
,∴N点的坐标为(
,
).
设抛物线在点N处的切线l的方程为y-
=m(x-
),.…5分
将y=2x2代入上式得2x2-mx+
-
=0,
∵直线l与抛物线C相切,∴△=m2-8(
-
)=0,∴m=k.
即l∥AB..…8分
(3)解:假设存在实数k,使
•
=0,则NA⊥NB,
又∵M是AB的中点,∴|MN|=
|AB|..…9分
由(1)知yM=
(y1+y2)=
+2.
∵MN⊥x轴,∴|MN|=|yM-yN|=
..…11分
又|AB|=
|x1-x2|=
•
..…13分
∴
=
•
,解得k=±2.
即存在k=±2,使
•
=0..…14分
 (1)解:将y=2x2化为x2=
(1)解:将y=2x2化为x2=| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
(2)证明:如图,设A(x1,2x12),B(x2,2x22),把y=kx+2代入y=2x2得2x2-kx-2=0,
由韦达定理得x1+x2=
| k |
| 2 |
∴xN=xM=
| x1+x2 |
| 2 |
| k |
| 4 |
| k |
| 4 |
| k2 |
| 8 |
设抛物线在点N处的切线l的方程为y-
| k2 |
| 8 |
| k |
| 4 |
将y=2x2代入上式得2x2-mx+
| mk |
| 4 |
| k2 |
| 8 |
∵直线l与抛物线C相切,∴△=m2-8(
| mk |
| 4 |
| k2 |
| 8 |
即l∥AB..…8分
(3)解:假设存在实数k,使
| NA |
| NB |
又∵M是AB的中点,∴|MN|=
| 1 |
| 2 |
由(1)知yM=
| 1 |
| 2 |
| k2 |
| 4 |
∵MN⊥x轴,∴|MN|=|yM-yN|=
| k2+16 |
| 8 |
又|AB|=
| 1+k2 |
| 1 |
| 2 |
| k2+1 |
| k2+16 |
∴
| k2+16 |
| 8 |
| 1 |
| 4 |
| k2+1 |
| k2+16 |
即存在k=±2,使
| NA |
| NB |
点评:本题考查抛物线方程与性质,考查直线与抛物线的位置关系,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
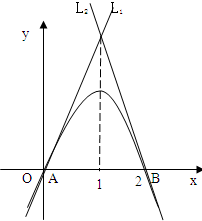 已知抛物线C:y=-x2+2x,在点A(0,0),B(2,0)分别作抛物线的切线L1、L2.
已知抛物线C:y=-x2+2x,在点A(0,0),B(2,0)分别作抛物线的切线L1、L2.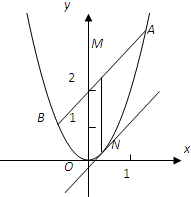 已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.