题目内容
本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分
(1)(本小题满分7分)选修4-2:矩阵与变换
变换 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
.
(Ⅰ)求变换 的矩阵;
的矩阵;
(Ⅱ)圆 在变换
在变换 的作用下变成了什么图形?
的作用下变成了什么图形?
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数).
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线 上有一定点
上有一定点 ,曲线
,曲线 与
与 交于M,N两点,求
交于M,N两点,求 的值.
的值.
(3)(本小题满分7分)选修4-5:不等式选讲
已知 为实数,且
为实数,且
(Ⅰ)求证:
(Ⅱ)求实数m的取值范围.
【答案】
(1)解:(Ⅰ)由已知得T:
∴变化T的矩阵是∴ ……3分
……3分
(Ⅱ)由 得:
得: ………………………4分
………………………4分
代入方程 ,得:
,得: ………………………6分
………………………6分
∴圆C:  在变化T的作用下变成了椭圆
在变化T的作用下变成了椭圆 ……………………7分
……………………7分
(2)解:(Ⅰ)由 得
得
即 ,从而
,从而
整理得 ………………………………… 3分
………………………………… 3分
(Ⅱ)把直线的参数方程代入到曲线 的直角坐标方程,得
的直角坐标方程,得
 .由
.由 的几何意义知
的几何意义知 ……………… 7分
……………… 7分
(3)解:(Ⅰ)由柯西不等式得 ………2分
………2分
即 …………4分
…………4分
(Ⅱ)由已知得
 …………6分
…………6分
又
 …………7分
…………7分
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
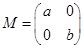 (其中a>0,b>0).
(其中a>0,b>0).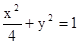 ,求a,b的值.
,求a,b的值. (其中a>0,b>0).
(其中a>0,b>0).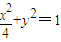 ,求a,b的值.
,求a,b的值. .
. ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;