题目内容
已知 =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)其中x∈[
=(sinx,2cosx)其中x∈[ ,
, ],设函数f(x)=
],设函数f(x)= •
• +|
+| |2+
|2+
(1)求函数f(x)的值域;
(2)若f(x)=8,求函数f(x- )的值.
)的值.
解:(1)∵ =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)
=(sinx,2cosx)
函数f(x)= •
• +|
+| |2+
|2+ =5
=5 cosx•sinx+2cosx•cosx+sin2x+4cos2x+
cosx•sinx+2cosx•cosx+sin2x+4cos2x+ …(2分)
…(2分)
=5 cosx•sinx+5cos2x+
cosx•sinx+5cos2x+
= sin2x+
sin2x+ cos2x+5
cos2x+5
=5sin(2x+ )+5 …(5分)
)+5 …(5分)
由∵x∈[ ,
, ],
],
∴ ≤2x+
≤2x+ ≤
≤ ,
,
∴- ≤sin(2x+
≤sin(2x+ )≤1…(7分)
)≤1…(7分)
即x∈[ ,
, ]时,函数f(x)的值域为[
]时,函数f(x)的值域为[ ,10]…(8分)
,10]…(8分)
(2)∵f(x)=5sin(2x+ )+5=8
)+5=8
则sin(2x+ )=
)= ,…(9分)
,…(9分)
又∵ ≤2x+
≤2x+ ≤
≤ ,
,
∴cos(2x+ )=-
)=- …(11分)
…(11分)
∴f(x- )=5sin2x+5
)=5sin2x+5
=5sin(2x+ -
- )+5
)+5
=5[sin(2x+ )cos
)cos -cos(2x+
-cos(2x+ )sin
)sin ]+5
]+5
=5( •
• +
+ •
• )+5
)+5
= +7 …(14分)
+7 …(14分)
分析:(1)由已知中 =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)设函数f(x)=
=(sinx,2cosx)设函数f(x)= •
• +|
+| |2+
|2+ ,根据平面向量的数量积公式,我们易求出函数f(x)的解析式,进而根据二倍角公式和辅助角公式,可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数的图象和性质及其中x∈[
,根据平面向量的数量积公式,我们易求出函数f(x)的解析式,进而根据二倍角公式和辅助角公式,可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数的图象和性质及其中x∈[ ,
, ],求出函数f(x)的值域;
],求出函数f(x)的值域;
(2)根据(1)中函数的解析式,及f(x)=8 我们可以求出2x+ 的正弦值,进而根据2x+
的正弦值,进而根据2x+ 的范围求出其余弦值,进而根据f(x-
的范围求出其余弦值,进而根据f(x- )=5sin2x+5=5sin(2x+
)=5sin2x+5=5sin(2x+ -
- )+5结合两角差的正弦公式得到答案.
)+5结合两角差的正弦公式得到答案.
点评:本题考查的知识点是平面向量的数量积运算,三角函数的图象和性质,二倍角公式,辅助角公式,是平面向量和三角函数比较综合的应用,其中根据平面向量的数量积公式、二倍角公式和辅助角公式,求出函数f(x)的解析式是解答本题的关键.
 =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)
=(sinx,2cosx)函数f(x)=
 •
• +|
+| |2+
|2+ =5
=5 cosx•sinx+2cosx•cosx+sin2x+4cos2x+
cosx•sinx+2cosx•cosx+sin2x+4cos2x+ …(2分)
…(2分)=5
 cosx•sinx+5cos2x+
cosx•sinx+5cos2x+
=
 sin2x+
sin2x+ cos2x+5
cos2x+5=5sin(2x+
 )+5 …(5分)
)+5 …(5分)由∵x∈[
 ,
, ],
],∴
 ≤2x+
≤2x+ ≤
≤ ,
,∴-
 ≤sin(2x+
≤sin(2x+ )≤1…(7分)
)≤1…(7分)即x∈[
 ,
, ]时,函数f(x)的值域为[
]时,函数f(x)的值域为[ ,10]…(8分)
,10]…(8分)(2)∵f(x)=5sin(2x+
 )+5=8
)+5=8则sin(2x+
 )=
)= ,…(9分)
,…(9分)又∵
 ≤2x+
≤2x+ ≤
≤ ,
,∴cos(2x+
 )=-
)=- …(11分)
…(11分)∴f(x-
 )=5sin2x+5
)=5sin2x+5=5sin(2x+
 -
- )+5
)+5=5[sin(2x+
 )cos
)cos -cos(2x+
-cos(2x+ )sin
)sin ]+5
]+5=5(
 •
• +
+ •
• )+5
)+5=
 +7 …(14分)
+7 …(14分)分析:(1)由已知中
 =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)设函数f(x)=
=(sinx,2cosx)设函数f(x)= •
• +|
+| |2+
|2+ ,根据平面向量的数量积公式,我们易求出函数f(x)的解析式,进而根据二倍角公式和辅助角公式,可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数的图象和性质及其中x∈[
,根据平面向量的数量积公式,我们易求出函数f(x)的解析式,进而根据二倍角公式和辅助角公式,可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数的图象和性质及其中x∈[ ,
, ],求出函数f(x)的值域;
],求出函数f(x)的值域;(2)根据(1)中函数的解析式,及f(x)=8 我们可以求出2x+
 的正弦值,进而根据2x+
的正弦值,进而根据2x+ 的范围求出其余弦值,进而根据f(x-
的范围求出其余弦值,进而根据f(x- )=5sin2x+5=5sin(2x+
)=5sin2x+5=5sin(2x+ -
- )+5结合两角差的正弦公式得到答案.
)+5结合两角差的正弦公式得到答案.点评:本题考查的知识点是平面向量的数量积运算,三角函数的图象和性质,二倍角公式,辅助角公式,是平面向量和三角函数比较综合的应用,其中根据平面向量的数量积公式、二倍角公式和辅助角公式,求出函数f(x)的解析式是解答本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
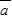 =(5
=(5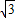 cosx,cosx),
cosx,cosx),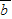 =(sinx,2cosx)其中x∈[
=(sinx,2cosx)其中x∈[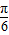 ,
,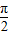 ],设函数f(x)=
],设函数f(x)=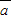 •
•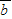 +|
+| |2+
|2+
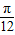 )的值.
)的值.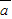 =(5
=(5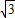 cosx,cosx),
cosx,cosx),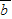 =(sinx,2cosx)其中x∈[
=(sinx,2cosx)其中x∈[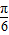 ,
,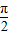 ],设函数f(x)=
],设函数f(x)=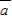 •
•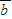 +|
+|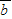 |2+
|2+
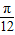 )的值.
)的值.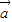 =(5
=(5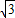 cosx,cosx),
cosx,cosx),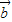 =(sinx,2cosx),函数f(x)=
=(sinx,2cosx),函数f(x)=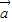
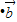 +
+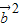 .
.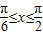 时,求函数f(x)的值域.
时,求函数f(x)的值域.