题目内容
下列命题中:
(1)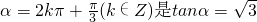 的充分不必要条件;
的充分不必要条件;
(2)函数f(x)=|2cosx-1|的最小正周期是π;
(3)△ABC中,若cosAcosB>sinAsinB,则△ABC为钝角三角形;
(4)若a+b=0,则函数y=asinx-bcosx的图象的一条对称轴方程为 ;
;
其中是真命题的为________.
解:对于(1)若“ ”成立则能推出“
”成立则能推出“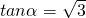 ”成立,反之若“
”成立,反之若“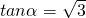 ”成立,则有
”成立,则有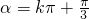 即推不出“
即推不出“ ”成立,所以
”成立,所以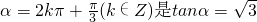 的充分不必要条件;故(1)对
的充分不必要条件;故(1)对
对于(2)函数f(x)=|2cosx-1|的最小正周期是2π故(2)错
对于(3),若cosAcosB>sinAsinB则cos(A+B)>0则A+B为锐角,则C为钝角,则△ABC为钝角三角形故(3)对
对于(4),∵a+b=0∴a=-b∴y=asinx-bcosx=a(sinx+cosx)=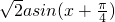 ∴
∴ 是图象的一条对称轴
是图象的一条对称轴
故(4)对
故答案为(1)(3)(4)
分析:根据题意,依次分析命题可得:利用充要条件的判断方法得到(1)对;通过画图形求出函数的周期得到(2)错;通过两角和的余弦公式及三角形的内角和判断出(3)对;利用三角函数的公式 及整体角处理的方法研究三角函数的性质判断出(4)对,综合可得答案.
及整体角处理的方法研究三角函数的性质判断出(4)对,综合可得答案.
点评:本题考查如何判断条件问题、考查三角函数周期的求法、考查两角和的余弦公式及三角形的内角和公式、开始三角函数的重要公式 、考查整体角处理的思想方法.
、考查整体角处理的思想方法.
 ”成立则能推出“
”成立则能推出“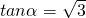 ”成立,反之若“
”成立,反之若“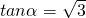 ”成立,则有
”成立,则有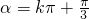 即推不出“
即推不出“ ”成立,所以
”成立,所以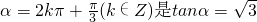 的充分不必要条件;故(1)对
的充分不必要条件;故(1)对对于(2)函数f(x)=|2cosx-1|的最小正周期是2π故(2)错
对于(3),若cosAcosB>sinAsinB则cos(A+B)>0则A+B为锐角,则C为钝角,则△ABC为钝角三角形故(3)对
对于(4),∵a+b=0∴a=-b∴y=asinx-bcosx=a(sinx+cosx)=
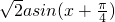 ∴
∴ 是图象的一条对称轴
是图象的一条对称轴故(4)对
故答案为(1)(3)(4)
分析:根据题意,依次分析命题可得:利用充要条件的判断方法得到(1)对;通过画图形求出函数的周期得到(2)错;通过两角和的余弦公式及三角形的内角和判断出(3)对;利用三角函数的公式
 及整体角处理的方法研究三角函数的性质判断出(4)对,综合可得答案.
及整体角处理的方法研究三角函数的性质判断出(4)对,综合可得答案.点评:本题考查如何判断条件问题、考查三角函数周期的求法、考查两角和的余弦公式及三角形的内角和公式、开始三角函数的重要公式
 、考查整体角处理的思想方法.
、考查整体角处理的思想方法. 
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
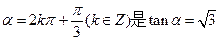 的充分不必要条件;
的充分不必要条件;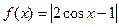 的最小正周期是
的最小正周期是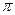 ;
; 中,若
中,若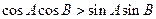 ,则
,则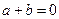 ,则函数
,则函数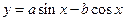 的图像的一条对称轴方程为
的图像的一条对称轴方程为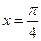 ;
;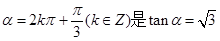 的充分不必要条件;
的充分不必要条件;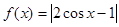 的最小正周期是
的最小正周期是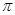 ;
; 中,若
中,若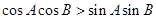 ,则
,则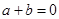 ,则函数
,则函数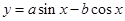 的图像的一条对称轴方程为
的图像的一条对称轴方程为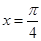 ;
;