题目内容
函数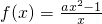 在区间(0,+∞)上单调递增,那么实数a的取值范围是
在区间(0,+∞)上单调递增,那么实数a的取值范围是
- A.a≥0
- B.a>0
- C.a≤0
- D.a<0
A
分析:先求函数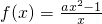 的导数,根据函数的增区间上导数大于0,可知,若函数
的导数,根据函数的增区间上导数大于0,可知,若函数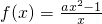 在区间(0,+∞)上单调递增,则x∈(0,+∞)时,f′(x)>0恒成立,再通过分类讨论a为何值时f′(x)>0恒成立即可求出a的范围.
在区间(0,+∞)上单调递增,则x∈(0,+∞)时,f′(x)>0恒成立,再通过分类讨论a为何值时f′(x)>0恒成立即可求出a的范围.
解答:f′(x)= =
=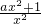 ,
,
∵函数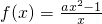 在区间(0,+∞)上单调递增,∴当x∈(0,+∞)时,f′(x)>0恒成立.
在区间(0,+∞)上单调递增,∴当x∈(0,+∞)时,f′(x)>0恒成立.
即当x∈(0,+∞)时,ax2+1>0恒成立,
当a>0时,y=ax2+1的图象为开口向上,最低点为(0,1)的抛物线,∴当x∈(0,+∞)时,ax2+1>0恒成立.
当a=0时,1>0恒成立.
当a<0时,y=ax2+1的图象为开口向下,最高点为(0,1)的抛物线,∴当x∈(0,+∞)时,ax2+1>0不恒成立.
∴实数a的取值范围是a≥0,
故选A
点评:本题主要考查函数的单调性与导数之间的关系,在函数的单调增区间上导数大于0恒成立.
分析:先求函数
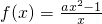 的导数,根据函数的增区间上导数大于0,可知,若函数
的导数,根据函数的增区间上导数大于0,可知,若函数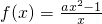 在区间(0,+∞)上单调递增,则x∈(0,+∞)时,f′(x)>0恒成立,再通过分类讨论a为何值时f′(x)>0恒成立即可求出a的范围.
在区间(0,+∞)上单调递增,则x∈(0,+∞)时,f′(x)>0恒成立,再通过分类讨论a为何值时f′(x)>0恒成立即可求出a的范围.解答:f′(x)=
 =
=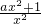 ,
,∵函数
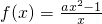 在区间(0,+∞)上单调递增,∴当x∈(0,+∞)时,f′(x)>0恒成立.
在区间(0,+∞)上单调递增,∴当x∈(0,+∞)时,f′(x)>0恒成立.即当x∈(0,+∞)时,ax2+1>0恒成立,
当a>0时,y=ax2+1的图象为开口向上,最低点为(0,1)的抛物线,∴当x∈(0,+∞)时,ax2+1>0恒成立.
当a=0时,1>0恒成立.
当a<0时,y=ax2+1的图象为开口向下,最高点为(0,1)的抛物线,∴当x∈(0,+∞)时,ax2+1>0不恒成立.
∴实数a的取值范围是a≥0,
故选A
点评:本题主要考查函数的单调性与导数之间的关系,在函数的单调增区间上导数大于0恒成立.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
设y=8x2-lnx,则此函数在区间(0,
)和(
,1)内分别( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、单调递增,单调递减 |
| B、单调递增,单调递增 |
| C、单调递减,单调递增 |
| D、单调递减,单调递减 |