题目内容
若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,则实数k的取值范围是( )
| A、(-∞,3] | B、[9,+∞) | C、(0,9] | D、(-∞,9] |
分析:①当k≤0时,联立方程组,根据判别式△<0,可得两个函数的图象无交点,故满足条件.②当k>0时,在同一个坐标系中,画出这两个函数的图,
如图所示:数形结合可得 0<
≤3,由此求得k的范围.综合①②可得k的范围.
如图所示:数形结合可得 0<
| k |
解答: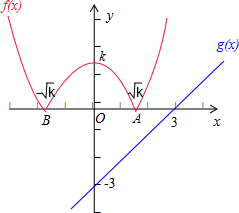 解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y=
解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y=
,可得x2-3x+3-k=0.
由于判别式△=1-4(3-k)=-11+4k<0,故x2-3x+3-k=0无解,
故函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象无交点,故满足条件.
②当k>0时,在同一个坐标系中,画出函数f(x)=|x2-k|的图象(红线部分)
与函数g(x)=x-3的图象(绿线部分),
如图所示:
此时,若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,
则有 0<
≤3,∴0<k≤9.
综合①②可得,k≤9,
故选 D.
 解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y=
解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y=
|
由于判别式△=1-4(3-k)=-11+4k<0,故x2-3x+3-k=0无解,
故函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象无交点,故满足条件.
②当k>0时,在同一个坐标系中,画出函数f(x)=|x2-k|的图象(红线部分)
与函数g(x)=x-3的图象(绿线部分),
如图所示:
此时,若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,
则有 0<
| k |
综合①②可得,k≤9,
故选 D.
点评:本题主要考查两个函数的图象的交点个数的判断,体现了分类讨论以及数形结合的数学思想,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
若函数f(x)(x∈R)为奇函数,且存在反函数f-1(x)(与f(x)不同),F(x)=
,则下列关于函数F(x)的奇偶性的说法中正确的是( )
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F(x)是奇函数非偶函数 |
| B、F(x)是偶函数非奇函数 |
| C、F(x)既是奇函数又是偶函数 |
| D、F(x)既非奇函数又非偶函数 |