题目内容
已知抛物线x2=2py (p>0),过点M (0,- )向抛物线引两条切线,A、B为切点,则线段AB的长度是
)向抛物线引两条切线,A、B为切点,则线段AB的长度是
- A.2p
- B.p
- C.
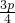
- D.

A
分析:设过M(0,- )与抛物线x2=2py (p>0)相切的直线l的斜率为k,可求得l的方程为:y=kx-
)与抛物线x2=2py (p>0)相切的直线l的斜率为k,可求得l的方程为:y=kx- ,与抛物线x2=2py (p>0)联立,整理成关于x的一元二次方程,由△=0可求得k,从而可求得切点A、B的坐标,由两点间的距离公式可求得线段AB的长度.
,与抛物线x2=2py (p>0)联立,整理成关于x的一元二次方程,由△=0可求得k,从而可求得切点A、B的坐标,由两点间的距离公式可求得线段AB的长度.
解答:由题意可知,过点M(0,- )与抛物线x2=2py (p>0)相切的直线l的斜率存在,设为k,则l的方程为:y=kx-
)与抛物线x2=2py (p>0)相切的直线l的斜率存在,设为k,则l的方程为:y=kx- ,与抛物线方程x2=2py (p>0)联立,
,与抛物线方程x2=2py (p>0)联立,
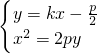 消掉y得:x2-2pkx+p2=0,
消掉y得:x2-2pkx+p2=0,
∵直线l与抛物线x2=2py (p>0)相切,
∴△=4p2k2-4p2=0,解得k=±1;
当k=1时,解得x=p,y= ,
,
∴切点A的坐标为(p, );
);
同理可求,当k=-1时,切点B的坐标为(-p, );
);
∴|AB|=|p-(-p)|=2p.
故选A.
点评:本题考查直线与圆锥曲线的关系,将直线与圆锥曲线相切问题转化为二曲线构成的方程组有唯一解的问题,着重考查方程思想与转化思想,属于中档题.
分析:设过M(0,-
 )与抛物线x2=2py (p>0)相切的直线l的斜率为k,可求得l的方程为:y=kx-
)与抛物线x2=2py (p>0)相切的直线l的斜率为k,可求得l的方程为:y=kx- ,与抛物线x2=2py (p>0)联立,整理成关于x的一元二次方程,由△=0可求得k,从而可求得切点A、B的坐标,由两点间的距离公式可求得线段AB的长度.
,与抛物线x2=2py (p>0)联立,整理成关于x的一元二次方程,由△=0可求得k,从而可求得切点A、B的坐标,由两点间的距离公式可求得线段AB的长度.解答:由题意可知,过点M(0,-
 )与抛物线x2=2py (p>0)相切的直线l的斜率存在,设为k,则l的方程为:y=kx-
)与抛物线x2=2py (p>0)相切的直线l的斜率存在,设为k,则l的方程为:y=kx- ,与抛物线方程x2=2py (p>0)联立,
,与抛物线方程x2=2py (p>0)联立,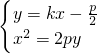 消掉y得:x2-2pkx+p2=0,
消掉y得:x2-2pkx+p2=0,∵直线l与抛物线x2=2py (p>0)相切,
∴△=4p2k2-4p2=0,解得k=±1;
当k=1时,解得x=p,y=
 ,
,∴切点A的坐标为(p,
 );
);同理可求,当k=-1时,切点B的坐标为(-p,
 );
);∴|AB|=|p-(-p)|=2p.
故选A.
点评:本题考查直线与圆锥曲线的关系,将直线与圆锥曲线相切问题转化为二曲线构成的方程组有唯一解的问题,着重考查方程思想与转化思想,属于中档题.

练习册系列答案
相关题目
 (2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2
(2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2