题目内容
 如图,在正四面体ABCD中,E为AB的中点,F为CD的中点,则异面直线EF与AC所成的角为
如图,在正四面体ABCD中,E为AB的中点,F为CD的中点,则异面直线EF与AC所成的角为
- A.90°
- B.60°
- C.45°
- D.30°
C
分析:根据正四面体的性质,每条棱都相等,相对的棱互相垂直,可借助中位线,平移直线AC,得到异面直线EF与AC所成的角,再放入直角三角形中,即可求得.
解答: 解:取BC的中点G,连接EG,FG,
解:取BC的中点G,连接EG,FG,
∵E,G分别为AB,BC的中点,
∴EG∥AC,FG∥BD,EG=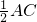 ,FG=
,FG=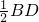
∴∠FEG为异面直线EF与AC所成的角
∵四面体ABCD为正四面体,
∴AC=BD,
∴EG=FG
过点A作AO⊥平面BCD,垂足为O,则O为△BCD的重心,AO⊥BD
∵CO⊥BD,AO∩CO=O
∴BD⊥平面AOC
∵AC?平面AOC
∴BD⊥AC
∵EG∥AC,FG∥BD
∴EG⊥FG
在Rt△EGF中,∵∠EGF=90°,且EG=FG
∴∠FEG=45°
故选C
点评:本题主要考查了正四面体中线线位置关系,以及异面直线所成角的求法,综合考查了学生的识图能力,作图能力,以及空间想象力.
分析:根据正四面体的性质,每条棱都相等,相对的棱互相垂直,可借助中位线,平移直线AC,得到异面直线EF与AC所成的角,再放入直角三角形中,即可求得.
解答:
 解:取BC的中点G,连接EG,FG,
解:取BC的中点G,连接EG,FG,∵E,G分别为AB,BC的中点,
∴EG∥AC,FG∥BD,EG=
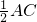 ,FG=
,FG=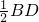
∴∠FEG为异面直线EF与AC所成的角
∵四面体ABCD为正四面体,
∴AC=BD,
∴EG=FG
过点A作AO⊥平面BCD,垂足为O,则O为△BCD的重心,AO⊥BD
∵CO⊥BD,AO∩CO=O
∴BD⊥平面AOC
∵AC?平面AOC
∴BD⊥AC
∵EG∥AC,FG∥BD
∴EG⊥FG
在Rt△EGF中,∵∠EGF=90°,且EG=FG
∴∠FEG=45°
故选C
点评:本题主要考查了正四面体中线线位置关系,以及异面直线所成角的求法,综合考查了学生的识图能力,作图能力,以及空间想象力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,在正四面体ABCD中,E为AB的中点,F为CD的中点,则异面直线EF与AC所成的角为( )
如图,在正四面体ABCD中,E为AB的中点,F为CD的中点,则异面直线EF与AC所成的角为( )


