题目内容
在△ABC中,三个内角A,B,C的对边分别为a,b,c.若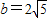 ,
,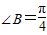 ,
,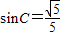 ,则c= ;a= .
,则c= ;a= .
【答案】分析:根据正弦定理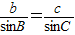 的式子,代入题中数据解出c=
的式子,代入题中数据解出c=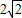 .再由余弦定理b2=a2+c2-2accosB的式子,代入数据解关于a的方程,即可得到a=6.
.再由余弦定理b2=a2+c2-2accosB的式子,代入数据解关于a的方程,即可得到a=6.
解答:解:∵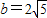 ,
,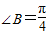 ,
,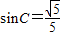 ,
,
∴根据正弦定理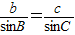 ,得c=
,得c=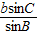 =
=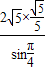 =
=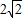
由余弦定理b2=a2+c2-2accosB,得
20=a2+8-2a×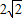 ×cos
×cos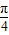 ,整理得a2-4a-12=0
,整理得a2-4a-12=0
解之得a=6(舍负)
故答案为: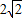 ,6
,6
点评:本题给出三角形的两个角和其中一个角的对边,求另一角的对边并由此求第三边长.着重考查了利用正余弦定理解三角形的知识,属于中档题.
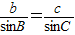 的式子,代入题中数据解出c=
的式子,代入题中数据解出c=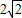 .再由余弦定理b2=a2+c2-2accosB的式子,代入数据解关于a的方程,即可得到a=6.
.再由余弦定理b2=a2+c2-2accosB的式子,代入数据解关于a的方程,即可得到a=6.解答:解:∵
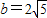 ,
,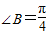 ,
,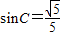 ,
,∴根据正弦定理
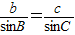 ,得c=
,得c=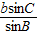 =
=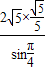 =
=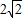
由余弦定理b2=a2+c2-2accosB,得
20=a2+8-2a×
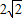 ×cos
×cos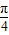 ,整理得a2-4a-12=0
,整理得a2-4a-12=0解之得a=6(舍负)
故答案为:
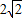 ,6
,6点评:本题给出三角形的两个角和其中一个角的对边,求另一角的对边并由此求第三边长.着重考查了利用正余弦定理解三角形的知识,属于中档题.

练习册系列答案
相关题目