题目内容

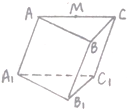在斜三棱柱ABC-A1B1C1中，AC的中点为M，
B1A1
=
a
，
B1C1
=
b
，
AA1
=
c
，则
B1M
=
1
2
(
a
+
b
)+
c
1
2
(
a
+
b
)+
c
．（用
a
，
b
，
c
表示）
分析：根据平面向量加法的意义，可得
B 1A
=
B1A1
+
BB 1
，
B 1C
=
B1C1
+
BB 1
，在三角形B1AC中可得
B1M
=
1
2
(
B1A 
+
B 1C
)，将前面两个等式代入再利用已知条件化简可得
B1M
=
1
2
(
a
+
b
)+
c
，问题解决．
解答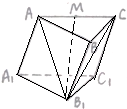：解：在平行四边形A1ABB1中，根据向量的加法法则得
B 1A
=
B1A1
+
BB 1
=
c
+
a

同理，在平行四边形B1C1CB中得
B 1C
=
B1C1
+
BB 1
=
c
+
b

在△B1AC中，B1M是中线，
所以
B1M
=
1
2
(
B1A 
+
B 1C
)=
1
2
(
c
+
a
)+(
c
+
b
)=
1
2
(
a
+
b
)+
c

即
B1M
=
1
2
(
a
+
b
)+
c

故答案为
1
2
(
a
+
b
)+
c
点评：本题着重考查了向量在几何方面的应用，属于中档题．能够熟练地运用平面向量的平行四边形法则和三角形法则，将未知向量用已知向量表示，逐步得到我们要求的向量的表达式，是解决本题的关键．
练习册系列答案
相关题目
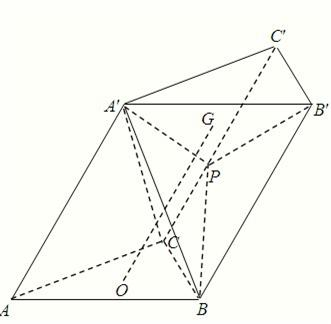精英家教网在斜三棱柱ABC-A′B′C′中，底面△ABC为正三角形，设AA′：AC=λ．顶点A′在底面ABC上的射影O是△ABC的中心，P为侧棱CC′中点，G为△PA′B′的重心．
（Ⅰ）求证：OG∥平面AA′B′B；
（Ⅱ）当λ=
2
时，求证：平面A′B′P⊥平面BB′C′C；
（Ⅲ）当λ=1时，求二面角C-A′B-P的大小．
（2008•武汉模拟）如图，在斜三棱柱ABC-A'B'C'中，∠ABC=90°，则侧面A'ACC'⊥侧面ABC，又AA'和底面所成60°的角，且AA'=2a，AB=BC=
2
a．
（1）求平面ABB'A'与底面ABC所成的角的正切值；
（2）求侧面BB'C'C的面积．
在斜三棱柱ABC-A′B′C′中，底面△ABC为正三角形，设AA′：AC=λ．顶点A′在底面ABC上的射影O是△ABC的中心，P为侧棱CC′中点，G为△PA′B′的重心．
（Ⅰ）求证：OG∥平面AA′B′B；
（Ⅱ）当λ=时，求证：平面A′B′P⊥平面BB′C′C；
（Ⅲ）当λ=1时，求二面角C-A′B-P的大小．
在斜三棱柱ABC-A′B′C′中，底面△ABC为正三角形，设AA′：AC=λ．顶点A′在底面ABC上的射影O是△ABC的中心，P为侧棱CC′中点，G为△PA′B′的重心．
（Ⅰ）求证：OG∥平面AA′B′B；
（Ⅱ）当λ=时，求证：平面A′B′P⊥平面BB′C′C；
（Ⅲ）当λ=1时，求二面角C-A′B-P的大小．
如图，在斜三棱柱ABC-A'B'C'中，∠ABC=90°，则侧面A'ACC'⊥侧面ABC，又AA'和底面所成60°的角，且AA'=2a，AB=BC=．
（1）求平面ABB'A'与底面ABC所成的角的正切值；
（2）求侧面BB'C'C的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网