题目内容
已知椭圆C:
+
=1(a>b>0)的右焦点为F,离心率为
,长轴长小于4
,点A在直线x=2上,且FA的最小值为1.
(1)求椭圆C的方程;
(2)点P(x0,y0)是椭圆C上第一象限内的点,O是坐标原点,直线OP与椭圆C的另一交点为Q,点T在C上,且PT⊥PQ;
①若PT的斜率为k,QT的斜率为k1,问kk1是否为定值,若为定值,求出kk1;若不是定值,说明理由.
②若QT交x轴于M,求△PQM的面积的最大值,并写出此时T点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(1)求椭圆C的方程;
(2)点P(x0,y0)是椭圆C上第一象限内的点,O是坐标原点,直线OP与椭圆C的另一交点为Q,点T在C上,且PT⊥PQ;
①若PT的斜率为k,QT的斜率为k1,问kk1是否为定值,若为定值,求出kk1;若不是定值,说明理由.
②若QT交x轴于M,求△PQM的面积的最大值,并写出此时T点的坐标.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设出右焦点,运用离心率公式,得到b=c,由点到直线的距离公式,得到方程,解得即可得到c,再由a,b,c的关系,即可得到a,b,进而得到椭圆方程;
(2)①运用斜率公式和点差法,即可得到定值;
②运用直线方程,求出M,再由面积公式,即可得到△PQM的面积,再由椭圆的参数方程,结合二倍角公式,即可得到最大值,进而得到点P的坐标,再由PT的方程,联立椭圆方程,即可解得交点T.
(2)①运用斜率公式和点差法,即可得到定值;
②运用直线方程,求出M,再由面积公式,即可得到△PQM的面积,再由椭圆的参数方程,结合二倍角公式,即可得到最大值,进而得到点P的坐标,再由PT的方程,联立椭圆方程,即可解得交点T.
解答:
解:(1)设右焦点为F(c,0),
由于离心率为
,则b=c,a=
c,由于长轴长小于4
,即a<2
.
由于点A在直线x=2上,且FA的最小值为1,则|c-2|=1,解得,c=3或1.
由于c<2,则c=1,a=
,b=1,
则椭圆方程为:
+y2=1;
(2)①点P(x0,y0)是椭圆C上第一象限内的点,则x02+2y02=2,
直线OP与椭圆C的另一交点为Q,则为Q(-x0,-y0),
设T(x1,y1),则k=
,k1=
,则kk1=
由于x02+2y02=2,x12+2y12=2,两式相减可得,
(x12-x02)+2(y12-y02)=0,则有kk1=-
,则kk1为定值,且为-
;
②直线OP的方程为:y=-
x,k=-
,
直线QT:y+y0=-
(x+x0),令y=0,则x=-2ky0-x0=x0,即M(x0,0),
则△PQM的面积为△POM和△QOM的面积之和,即为S=
x0(y0+y0)=x0y0,
由椭圆方程的参数式,x0=
cosα,y0=sinα,
则有S=
sinαcosα=
sin2α≤
,
当sin2α=1,即有α=
,x0=1,y0=
,即P(1,
),
由PT:y-
=-
(x-1),
联立椭圆方程:
+y2=1,解得T(
,
)
此时△PQM的面积的最大值为
.
由于离心率为
| ||
| 2 |
| 2 |
| 2 |
| 2 |
由于点A在直线x=2上,且FA的最小值为1,则|c-2|=1,解得,c=3或1.
由于c<2,则c=1,a=
| 2 |
则椭圆方程为:
| x2 |
| 2 |
(2)①点P(x0,y0)是椭圆C上第一象限内的点,则x02+2y02=2,
直线OP与椭圆C的另一交点为Q,则为Q(-x0,-y0),
设T(x1,y1),则k=
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x0 |
| y12-y02 |
| x12-x02 |
由于x02+2y02=2,x12+2y12=2,两式相减可得,
(x12-x02)+2(y12-y02)=0,则有kk1=-
| 1 |
| 2 |
| 1 |
| 2 |
②直线OP的方程为:y=-
| 1 |
| k |
| x0 |
| y0 |
直线QT:y+y0=-
| 1 |
| 2k |
则△PQM的面积为△POM和△QOM的面积之和,即为S=
| 1 |
| 2 |
由椭圆方程的参数式,x0=
| 2 |
则有S=
| 2 |
| ||
| 2 |
| ||
| 2 |
当sin2α=1,即有α=
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
由PT:y-
| ||
| 2 |
| 2 |
联立椭圆方程:
| x2 |
| 2 |
| 7 |
| 5 |
| ||
| 10 |
此时△PQM的面积的最大值为
| ||
| 2 |
点评:本题考查椭圆的方程和性质,考查直线的斜率公式及运用,考查联立直线方程和椭圆方程求交点,运用点差法求斜率之积,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
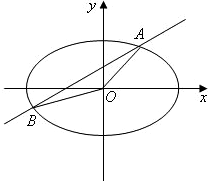 如图,直线y=x+b与椭圆
如图,直线y=x+b与椭圆