题目内容
在直角三角形ABC中,D是斜边BC上的一点,AB=AD,∠CAD=α,∠ABC=β,(1)求sinα+cos2β的值;
(2)若AC=
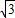 DC,求β的值.
DC,求β的值.
【答案】分析:(1)由于180°-2β+α=90°,可求得2β=90°+α,利用诱导公式可求得sinα+cos2β;
(2)在△ACD中利用正弦定理可求得sinβ=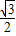 ,从而可求得β的值.
,从而可求得β的值.
解答:解:(1)由180°-2β+α=90°得2β-α=90°,
∴sinα+cos2β=sinα+cos(90°+α)=0.…(6分)
(2)在△ACD中由正弦定理得,
AC:DC=sin(180°-β):sinα,又因为AC=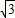 DC,
DC,
∴sinβ=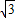 sinα,
sinα,
又∵sinα+cos2β=0,
∴2sin2β-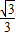 sinβ-1=0,
sinβ-1=0,
∴sinβ=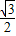 ,
,
又∵0<β<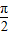 ,
,
∴β=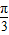 …(12分)
…(12分)
点评:本题考查正弦定理,考查分析与运算能力,求得sinβ=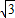 sinα是关键,属于中档题.
sinα是关键,属于中档题.
(2)在△ACD中利用正弦定理可求得sinβ=
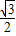 ,从而可求得β的值.
,从而可求得β的值.解答:解:(1)由180°-2β+α=90°得2β-α=90°,
∴sinα+cos2β=sinα+cos(90°+α)=0.…(6分)
(2)在△ACD中由正弦定理得,
AC:DC=sin(180°-β):sinα,又因为AC=
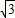 DC,
DC,∴sinβ=
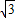 sinα,
sinα,又∵sinα+cos2β=0,
∴2sin2β-
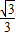 sinβ-1=0,
sinβ-1=0,∴sinβ=
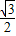 ,
,又∵0<β<
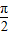 ,
,∴β=
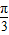 …(12分)
…(12分)点评:本题考查正弦定理,考查分析与运算能力,求得sinβ=
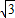 sinα是关键,属于中档题.
sinα是关键,属于中档题. 
练习册系列答案
相关题目


 如图,在直角三角形ABC中,D是斜边BC边上的中点,AC=8cm,BC=6cm,EC⊥平面ABC,EC=12cm,
如图,在直角三角形ABC中,D是斜边BC边上的中点,AC=8cm,BC=6cm,EC⊥平面ABC,EC=12cm,