题目内容
数列{an}的前n项和Sn满足Sn-Sn-1=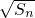 +
+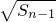 (n≥2),a1=1.
(n≥2),a1=1.
(1)证明:数列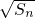 是等差数列.并求数列{an}的通项公式;
是等差数列.并求数列{an}的通项公式;
(2)若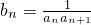 ,Tn=b1+b2+…+bn,求证:
,Tn=b1+b2+…+bn,求证: .
.
解:(1)∵ ,(n≥2)
,(n≥2)
又bn≥o, ,∴
,∴ ,
,
又 ,所以数列
,所以数列 是一个首项为1公差为1的等差数列.
是一个首项为1公差为1的等差数列.
 ,sn=n2.
,sn=n2.
当n≥2,an=Sn-Sn-1=n2-(n-1)2=2n-1;a1=1适合上式,∴an=2n-1(n∈N).
(2)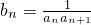 =
=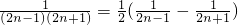 ,
,
Tn=b1+b2++bn
 ;
;
=
=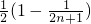
∵n∈N,∴ ,
, ,
, ,即
,即 .
.
分析:(1)利用平方差公式对题设中的等式化简整理求得 ,进而根据等差数列的定义判断出数列
,进而根据等差数列的定义判断出数列 是一个首项为1公差为1的等差数列.进而根据首项和公差求得数列
是一个首项为1公差为1的等差数列.进而根据首项和公差求得数列 的通项公式,进而根据an=Sn-Sn-1求得an.
的通项公式,进而根据an=Sn-Sn-1求得an.
(2)把(1)中的an代入bn,进而根据裂项法求得前n项的和,求得Tn=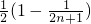 ,进而利用
,进而利用 推断出
推断出 ,原式得证.
,原式得证.
点评:本题主要考查了等差关系的确定和数列的求和,数列和不等式的综合运用.作为高考的必考内容,数列题常与不等式,函数等问题综合考查,综合性较强.
 ,(n≥2)
,(n≥2)又bn≥o,
 ,∴
,∴ ,
,又
 ,所以数列
,所以数列 是一个首项为1公差为1的等差数列.
是一个首项为1公差为1的等差数列. ,sn=n2.
,sn=n2.当n≥2,an=Sn-Sn-1=n2-(n-1)2=2n-1;a1=1适合上式,∴an=2n-1(n∈N).
(2)
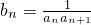 =
=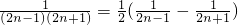 ,
,Tn=b1+b2++bn
 ;
;=

=
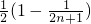
∵n∈N,∴
 ,
, ,
, ,即
,即 .
.分析:(1)利用平方差公式对题设中的等式化简整理求得
 ,进而根据等差数列的定义判断出数列
,进而根据等差数列的定义判断出数列 是一个首项为1公差为1的等差数列.进而根据首项和公差求得数列
是一个首项为1公差为1的等差数列.进而根据首项和公差求得数列 的通项公式,进而根据an=Sn-Sn-1求得an.
的通项公式,进而根据an=Sn-Sn-1求得an.(2)把(1)中的an代入bn,进而根据裂项法求得前n项的和,求得Tn=
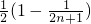 ,进而利用
,进而利用 推断出
推断出 ,原式得证.
,原式得证.点评:本题主要考查了等差关系的确定和数列的求和,数列和不等式的综合运用.作为高考的必考内容,数列题常与不等式,函数等问题综合考查,综合性较强.

练习册系列答案
相关题目