题目内容
若关于x的方程x2-2(1+i)x+
ab-(a-b)i=0(a、b∈R)至少有一个实根.(1)求a、b的范围;
(2)求方程实根的最大值和最小值.
解析:(1)设x0为原方程一实根,则x02-2(1+i)x0+ab-(a-b)i=0,?
故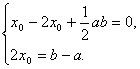
?
消去x0得(a+2)2+(b-2)2=8,?
故-
-2≤a≤
-2,2-
≤b≤2+
.?
(2)设a+2=
cosθ,b-2=
sinθ,??
则x0=
=2sin(θ-
)+2∈［0,4］,所以此方程实根的最大值为4,最小值为0.
练习册系列答案
相关题目
△ABC中三个内角为A、B、C，若关于x的方程x2-xcosAcosB-cos2
=0有一根为1，则△ABC一定是（ ）
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |