Question

（2008•广州二模）某工厂生产甲、乙两种产品，每生产一吨产品所消耗的电能和煤、所需工人人数以及所得产值如下表所示：

品种	电能（千度）	煤（吨）	工人人数（人）	产值（万元）
甲	2	3	5	7
乙	8	5	2	10

已知该工厂的工人人数最多是200人，根据限额，该工厂每天消耗电能不得超过160千度，消耗煤不得超过150吨，问怎样安排甲、乙两种产品的生产数量，才能使每天所得的产值最大．

Answer 1

分析：设设甲、乙两种产品每天分别生产x吨和y吨，每天所得的产值为z万元，依据题意，得约束条件和目标函数z=7x+10y，然后求得最优解，即求得所得的产值最大和最大值的状态．

解答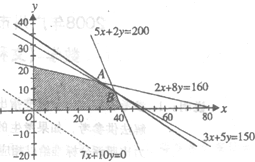：解：设甲、乙两种产品每天分别生产x吨和y吨，
则每天所得的产值z=7x+10y万元．…（2分）
依题意，得不等式

2x+8y≤160 3x+5y≤150 5x+2y≤200 x≥0 y≥0

（※）…（7分）
由

2x+8y=160 3x+5y=150

解得

x= 200 7 y= 90 7

由

5x+2y=200 3x+5y=150

解得

x= 700 19 y= 150 19

…（9分）
设点A的坐标为（

200

7

，

90

7

）点B的坐标为（

700

19

，

150

19

）则不等式组（※）所表示的平面区域是四边形的边界及其内部（如图中阴影部分）．
令z=0得7x+10y=0，作直线l₀：y=-

7

10

x由图可知把l₀平移至过点（

700

19

，

150

19

）
时，即

x= 700 19 y= 150 19

时，z取得最大值

6400

19

…（11分）
答：每天生产甲产

700

19

吨、乙产品

150

19

吨时．能获得最大的产值

6400

19

万元．…（12分）

点评：本小题考查线性规划等基础知识，考查综合运用知识分析问题和解决问题的能力．本题主要考查用简单的线性规划研究目标函数的最大和最小值，关键是通过平面区域，求得最优解，属于线性规划的应用题．