题目内容
7.设a∈[0,4],则使方程x2+ax+1=0有解的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 利用方程的解,求出a的范围,然后利用几何概型求解即可.
解答 解:方程x2+ax+1=0有解,可得a2-4≥0,解得a≥2,或a≤-2,
a∈[0,4],
使方程x2+ax+1=0有解的概率为:$\frac{1}{2}$.
故选:C.
点评 本题考查几何概型的求法,方程的解的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.圆x2+y2-2x+4y+3=0的圆心坐标为( )
| A. | (-2,4) | B. | (2,-4) | C. | (1,-2) | D. | (-1,2) |
16.如图,等腰三角形OAB(O为坐标原点)的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=$\frac{1}{2}$x交于点C,在△OAB中任取一点P,则点P落在△OBC中的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
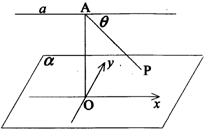 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..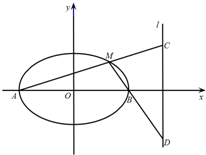 已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.
已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.