题目内容
已知等比数列{an}中,a2=2,a5=128.若bn=log2an,数列{bn}前n项的和为Sn.(Ⅰ)若Sn=35,求n的值;
(Ⅱ)求不等式Sn<2bn的解集.
【答案】分析:(Ⅰ)已知等比数列{an}中,设出公比为q,根据等比数列通项公式,代入a2=2,a5=128,求出公比,再利用等比数列的前n项和公式,代入Sn=35,求出n值;
(Ⅱ)因为bn=log2an,将an代入bn,求出其通项公式,代入不等式Sn<2bn求出n的范围;
解答:解:(Ⅰ)∵a2=a1q=2,a5=a1q4=128得q3=64,
∴q=4,a1=
∴an=a1qn-1=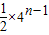 =22n-3,∴bn=log2an=log222n-3=2n-3
=22n-3,∴bn=log2an=log222n-3=2n-3
∵bn+1-bn=[2(n+1)-3]-(2n-3)=2
∴{bn}是以b1=-1为首项,2为公差数列;
∴Sn=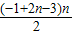 =35,即n2-2n-35=0,可得(n-7)(n+5)=0,
=35,即n2-2n-35=0,可得(n-7)(n+5)=0,
即n=7;
(Ⅱ)∵Sn-bn=n2-2n-(2n-3)=n2-4n+3<0
∴3-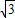 <n<3+
<n<3+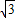 ,∵n∈N+,
,∵n∈N+,
∴n=2,3,4,即所求不等式的解集为{2,3,4};
点评:此题主要考查了等比数列的通项公式和等比数列的前n项和公式,此题计算量比较大,计算时要仔细,此题是一道基础题;
(Ⅱ)因为bn=log2an,将an代入bn,求出其通项公式,代入不等式Sn<2bn求出n的范围;
解答:解:(Ⅰ)∵a2=a1q=2,a5=a1q4=128得q3=64,
∴q=4,a1=

∴an=a1qn-1=
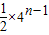 =22n-3,∴bn=log2an=log222n-3=2n-3
=22n-3,∴bn=log2an=log222n-3=2n-3∵bn+1-bn=[2(n+1)-3]-(2n-3)=2
∴{bn}是以b1=-1为首项,2为公差数列;
∴Sn=
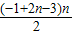 =35,即n2-2n-35=0,可得(n-7)(n+5)=0,
=35,即n2-2n-35=0,可得(n-7)(n+5)=0,即n=7;
(Ⅱ)∵Sn-bn=n2-2n-(2n-3)=n2-4n+3<0
∴3-
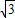 <n<3+
<n<3+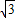 ,∵n∈N+,
,∵n∈N+,∴n=2,3,4,即所求不等式的解集为{2,3,4};
点评:此题主要考查了等比数列的通项公式和等比数列的前n项和公式,此题计算量比较大,计算时要仔细,此题是一道基础题;

练习册系列答案
相关题目