题目内容
已知函数f(x)= sin2x+2cos2x+1,
sin2x+2cos2x+1,
(1)求函数f(x)的单调递增区间;
(2)设△ABC的内角A,B,C对边分别为a,b,c,且c=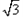 ,f(C)=3,若2sinA=sinB,求a,b的值。
,f(C)=3,若2sinA=sinB,求a,b的值。
 sin2x+2cos2x+1,
sin2x+2cos2x+1,(1)求函数f(x)的单调递增区间;
(2)设△ABC的内角A,B,C对边分别为a,b,c,且c=
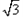 ,f(C)=3,若2sinA=sinB,求a,b的值。
,f(C)=3,若2sinA=sinB,求a,b的值。解:(1)∵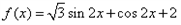
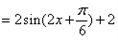 ,
,
令 ,解得
,解得 ,
,
∴f(x)的单调递增区间为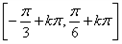
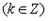 。
。
(2)由题意可知,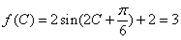 ,
,
∴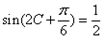 ,
,
∵0<C<π,
∴ 或
或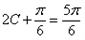 ,
,
即C=0(舍去)或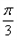 ,
,
∵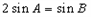 即
即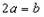 ,
,
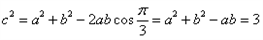 ,
,
解得a=1,b=2。
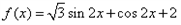
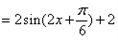 ,
,令
 ,解得
,解得 ,
, ∴f(x)的单调递增区间为
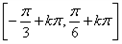
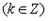 。
。(2)由题意可知,
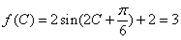 ,
, ∴
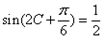 ,
, ∵0<C<π,
∴
 或
或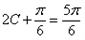 ,
,即C=0(舍去)或
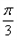 ,
,∵
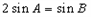 即
即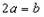 ,
, 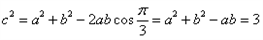 ,
,解得a=1,b=2。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
