题目内容
平面内动点 到定点
到定点 的距离比它到
的距离比它到 轴的距离大
轴的距离大 。
。
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)已知点A(3,2), 求 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.
(1) ;(2)最小值为
;(2)最小值为 ,此时
,此时 .
.
【解析】
试题分析:(1)根据抛物线的定义,所求动点 到定点
到定点 的距等于它到x=-1的距离,故答案为:
的距等于它到x=-1的距离,故答案为: ;(2)根据抛物线的定义,抛物线上的点
;(2)根据抛物线的定义,抛物线上的点 到焦点
到焦点 的距离等于其到准线的距离,所以
的距离等于其到准线的距离,所以
 ,得知当
,得知当 三点共线时,所求
三点共线时,所求 的值最小,此时
的值最小,此时 点坐标为
点坐标为 .
.
试题解析:(1)由题意,动点 到定点
到定点 的距等于它到x=-1的距离,由抛物线的定义知,p=2,所以所求的轨迹方程为
的距等于它到x=-1的距离,由抛物线的定义知,p=2,所以所求的轨迹方程为 .
.
(2)设点P在准线上的射影为D,记抛物线y2=2x的焦点为F(1,0),准线l是x= -1,由抛物线的定义知点P到焦点F的距离等于它到准线l的距离,即PF=PD ,
因此PA +PF=PA+ PD AD=4, 即当D,P,M三点共线时PA+PD最小,此时P(1,2)
AD=4, 即当D,P,M三点共线时PA+PD最小,此时P(1,2)
考点:1.抛物线的定义;2.与抛物线有关的最值.

练习册系列答案
相关题目
 的扇形的面积为( )
的扇形的面积为( ) B.
B.  C.
C.  D.
D.
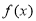 与
与 的各组中,是同一个关于x的函数的是( )
的各组中,是同一个关于x的函数的是( )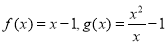
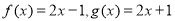
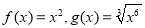

 是定义在区间
是定义在区间 上的奇函数,则
上的奇函数,则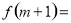 ( )
( )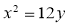 的焦点为
的焦点为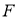 ,经过点
,经过点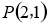 的直线
的直线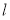 与抛物线相交于
与抛物线相交于 两点且点
两点且点 恰为
恰为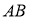 的中点,则
的中点,则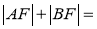 .
.
 平行,则它们之间的距离是( )
平行,则它们之间的距离是( ) D.4
D.4