题目内容
某船在海面A处测得灯塔C与A相距10
海里,且在北偏东30°的方向;测得灯塔B与A相距15
海里,且在北偏西75°的方向,船往正北方向航行到D处,再看灯塔B在南偏西60°的方向,问灯塔C与D相距多少海里?
| 3 |
| 6 |
分析:先画出草图,根据条件得到∠DBA=180°-∠BAD-∠BDA=45°,在三角形DBA中利用正弦定理求得DA的长,然后在三角形ADC中用余弦定理即可求出灯塔C与D相距多少海里.
解答:解: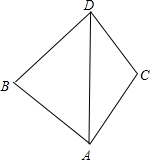 ∠BAD=75°,∠ADB=60°,∠DAC=30°,AB=15
∠BAD=75°,∠ADB=60°,∠DAC=30°,AB=15
,AC=10
.
∴∠DBA=180°-∠BAD-∠BDA=45°,
∴
=
⇒AD=
•sin∠DBA=30.
∴DC=
=
=10
.
所以灯塔C与D相距:10
海里
 ∠BAD=75°,∠ADB=60°,∠DAC=30°,AB=15
∠BAD=75°,∠ADB=60°,∠DAC=30°,AB=15| 6 |
| 3 |
∴∠DBA=180°-∠BAD-∠BDA=45°,
∴
| AD |
| sin∠DBA |
| AB |
| sin∠BDA |
| AB |
| sin∠BDA |
∴DC=
| AD2+AC2-2AC•AD•cos∠DAC |
302+(10
|
| 3 |
所以灯塔C与D相距:10
| 3 |
点评:本题主要考查正弦定理以及余弦定理在解三角形中的应用.解决此类问题的关键在于把文字语言转化为数学符号以及数学语言,用数学知识解题.

练习册系列答案
相关题目
 某船在海面A处测得灯塔D与A相距10
某船在海面A处测得灯塔D与A相距10 海里,且在北偏东
海里,且在北偏东 方向;测得灯塔B与A相距
方向;测得灯塔B与A相距 海里,且在北偏西
海里,且在北偏西 方向,船由A向正北方向航行到C处,测得灯塔B在南偏西
方向,船由A向正北方向航行到C处,测得灯塔B在南偏西 方向,这时灯塔D与C相距多少海里?D在C的什么方向?
方向,这时灯塔D与C相距多少海里?D在C的什么方向?
 某船在海面A处测得灯塔D与A相距10
某船在海面A处测得灯塔D与A相距10 海里,且在北偏东30°方向;测得灯塔B与A相距10
海里,且在北偏东30°方向;测得灯塔B与A相距10 海里,且在北偏西70°方向,船由A向正北方向航行到C处,测得灯塔B在南偏西60°方向,这时灯塔D与C相距多少海里?D在C的什么方向?
海里,且在北偏西70°方向,船由A向正北方向航行到C处,测得灯塔B在南偏西60°方向,这时灯塔D与C相距多少海里?D在C的什么方向?