题目内容
若f(x)是定义在[-2,2]上的奇函数,且在[0,2]上单调递减,若f(m)+f(2m-1)<0,则m的取值范围是
- A.

- B.

- C.
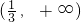
- D.
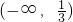
B
分析:首先要考虑函数的定义域,得出一个参数m的取值范围,然后在根据奇函数在对称区间上的单调性相同这一性质,得出在整个定义域上的单调情况,从而把原不等式通过移项,根据奇函数性质及单调性去掉函数符号,又得到一个参数m的取值范围,最后两个范围求交集可得最后的结果.
解答:∵f(x)定义域为[-2,2],
∴ ,解得-
,解得- ≤m≤
≤m≤ ①
①
又∵f(x)定义在[-2,2]上的奇函数,且在[0,2]上单调递减,
∴f(x)在[-2,0]上也单调递减,
∴f(x)在[-2,2]上单调递减,
又∵f(m)+f(2m-1)<0?f(2m-1)<-f(m)=f(-m),
∴2m-1>-m 即m> ②
②
由①②可知: <m≤
<m≤ .
.
故选B.
点评:本题主要考查了函数的单调性与奇偶性的性质,即:“奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反”.还要注意考虑定义域的问题,这一点常常容易忽略,所以本题也属于易错题,是一道中档题.
分析:首先要考虑函数的定义域,得出一个参数m的取值范围,然后在根据奇函数在对称区间上的单调性相同这一性质,得出在整个定义域上的单调情况,从而把原不等式通过移项,根据奇函数性质及单调性去掉函数符号,又得到一个参数m的取值范围,最后两个范围求交集可得最后的结果.
解答:∵f(x)定义域为[-2,2],
∴
 ,解得-
,解得- ≤m≤
≤m≤ ①
①又∵f(x)定义在[-2,2]上的奇函数,且在[0,2]上单调递减,
∴f(x)在[-2,0]上也单调递减,
∴f(x)在[-2,2]上单调递减,
又∵f(m)+f(2m-1)<0?f(2m-1)<-f(m)=f(-m),
∴2m-1>-m 即m>
 ②
②由①②可知:
 <m≤
<m≤ .
.故选B.
点评:本题主要考查了函数的单调性与奇偶性的性质,即:“奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反”.还要注意考虑定义域的问题,这一点常常容易忽略,所以本题也属于易错题,是一道中档题.

练习册系列答案
相关题目