题目内容
设函数y=x3-3ax2-24a2x+b有正的极大值和负的极小值,其差为4,
(1)求实数a的值;
(2)求b的取值范围.
解:(1)f'(x)=3x2-6ax-24a2
令f'(x)=0得x2-2ax-8a2=0
∴x1=4a,x2=-2a(2分)
∵f(4a)=b-80a3,f(-2a)=b+28a3,
∴|b-80a3-(b+28a3)|=4(4分)
∴ (6分)
(6分)
(2)当 时,
时,
得:f(-2a)>0,f(4a)<0,
∴ (8分)
(8分)
又 得:
得: (9分)
(9分)
同理当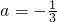 时,
时,
得:f(-2a)<0,f(4a)>0,
∴
又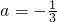 得,
得, (12分)
(12分)
∴当 得:
得: ;
;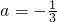 时,得
时,得 (14分)(结论2分)
(14分)(结论2分)
分析:(1)求导函数f'(x)=3x2-6ax-24a2,令f'(x)=0得x2-2ax-8a2=0,所以x1=4a,x2=-2a,利用极大值和极小值的差为4,可得|b-80a3-(b+28a3)|=4,从而可求求实数a的值;
(2)分类讨论:当 时,f(-2a)>0,f(4a)<0;当
时,f(-2a)>0,f(4a)<0;当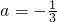 时,f(-2a)<0,f(4a)>0,从而可求b的取值范围.
时,f(-2a)<0,f(4a)>0,从而可求b的取值范围.
点评:本题以函数为载体,考查导数的运用,考查函数的单调性,考查函数的极值,考查分类讨论的数学思想,解题的关键是正确求导.
令f'(x)=0得x2-2ax-8a2=0
∴x1=4a,x2=-2a(2分)
∵f(4a)=b-80a3,f(-2a)=b+28a3,
∴|b-80a3-(b+28a3)|=4(4分)
∴
 (6分)
(6分)(2)当
 时,
时,| x | (-∞,-2a) | -2a | (-2a,4a) | 4a | (4a,+∞) |
| f(x) | + | 0 | - | 0 | + |
∴
 (8分)
(8分)又
 得:
得: (9分)
(9分)同理当
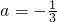 时,
时,| x | (-∞,-4a) | 4a | (4a,-2a) | -2a | (-2a,+∞) |
| f(x) | + | 0 | - | 0 | + |
∴

又
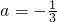 得,
得, (12分)
(12分)∴当
 得:
得: ;
;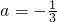 时,得
时,得 (14分)(结论2分)
(14分)(结论2分)分析:(1)求导函数f'(x)=3x2-6ax-24a2,令f'(x)=0得x2-2ax-8a2=0,所以x1=4a,x2=-2a,利用极大值和极小值的差为4,可得|b-80a3-(b+28a3)|=4,从而可求求实数a的值;
(2)分类讨论:当
 时,f(-2a)>0,f(4a)<0;当
时,f(-2a)>0,f(4a)<0;当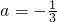 时,f(-2a)<0,f(4a)>0,从而可求b的取值范围.
时,f(-2a)<0,f(4a)>0,从而可求b的取值范围.点评:本题以函数为载体,考查导数的运用,考查函数的单调性,考查函数的极值,考查分类讨论的数学思想,解题的关键是正确求导.

练习册系列答案
相关题目