题目内容
某校高一(2)班共有学生51人,据统计原来每人每年用于购买饮料的平均支出是a元,若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用228元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图所示关系.(1)求y关于x的函数关系式;
(2)当a=120时,若该班每年需要纯净水380桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一种更少?说明你的理由;
(3)当a至少为多少时,该班学生集体改饮桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少?
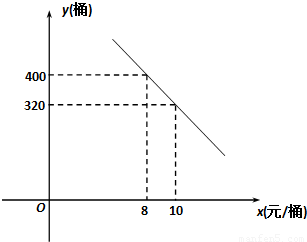
【答案】分析:(1)设出直线方程,根据题目中两组数据直接求出参数k,b,从而可得y关于x的函数关系式;
(2)分别比较两种方式花钱数量,判断哪一种花钱更少;
(3)设出每年购买纯净水的费用为P元与x的关系式,然后根据配方法求二次函数的最值.
解答:解:(1)设y=kx+b,
∵x=8时,y=400;x=10时,y=320.
∴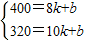 解之,得k=-40,b=720
解之,得k=-40,b=720
∴y与x的函数关系式为y=-40x+720(x>0);
(2)该班学生买饮料每年总费用为51×120=6120(元),
当y=380时,380=-40x+720,得x=8.5,
该班学生集体饮用桶装纯净水的每年总费用为380×8.5+228=3458(元),
显然,从经济上看饮用桶装纯净水花钱少;
(3)设该班每年购买纯净水的费用为P元,则P=xy=x(-40x+720)=-40(x-9)2+3240
∴x=9时,Pmax=3240
要使饮用桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少,则51a≥Pmax+228
解得a≥68,故a至少为68元时全班饮用桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少.
点评:本题考查函数模型的选取与应用,考查学生利用数学知识解决实际问题,通过题意分别列出等式,并根据二次函数求最值,属于中档题.
(2)分别比较两种方式花钱数量,判断哪一种花钱更少;
(3)设出每年购买纯净水的费用为P元与x的关系式,然后根据配方法求二次函数的最值.
解答:解:(1)设y=kx+b,
∵x=8时,y=400;x=10时,y=320.
∴
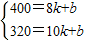 解之,得k=-40,b=720
解之,得k=-40,b=720∴y与x的函数关系式为y=-40x+720(x>0);
(2)该班学生买饮料每年总费用为51×120=6120(元),
当y=380时,380=-40x+720,得x=8.5,
该班学生集体饮用桶装纯净水的每年总费用为380×8.5+228=3458(元),
显然,从经济上看饮用桶装纯净水花钱少;
(3)设该班每年购买纯净水的费用为P元,则P=xy=x(-40x+720)=-40(x-9)2+3240
∴x=9时,Pmax=3240
要使饮用桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少,则51a≥Pmax+228
解得a≥68,故a至少为68元时全班饮用桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少.
点评:本题考查函数模型的选取与应用,考查学生利用数学知识解决实际问题,通过题意分别列出等式,并根据二次函数求最值,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
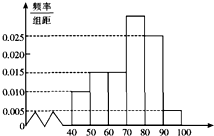 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 某校高一(2)班共有学生51人,据统计原来每人每年用于购买饮料的平均支出是a元,若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用228元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图所示关系.
某校高一(2)班共有学生51人,据统计原来每人每年用于购买饮料的平均支出是a元,若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用228元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图所示关系.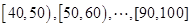 ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题: (3)现按照这六个分数段把学生分成六组(从低分段到高分段依次为第一组、第二组、…、第六组),为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差不小于30分(以分数段中点值为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求任选两组为“最佳组合”的概率.
(3)现按照这六个分数段把学生分成六组(从低分段到高分段依次为第一组、第二组、…、第六组),为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差不小于30分(以分数段中点值为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求任选两组为“最佳组合”的概率.