题目内容
下列四个函数中，在区间
上为减函数的是
- A.y=xe-x
- B.
- C.y=xlnx
- D.
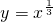
C
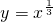分析：求出y=xlnx与y=xe-x的导函数，判断出导函数的符号，利用导函数小于0，函数单减，函数大于0，函数单增，判断出函数的单调性，利用基本初等函数的单调性判断出与的单调性．
解答：对于
∵
为R上的减函数，所以为R上的增函数
对于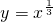是R上的增函数
对于y=xe-x
∵y′=（1-x）e-x
∵
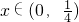
∴y′＞0
故y=xe-x在为增函数
对于y=xlnx
∵
∴
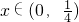
∴y′＜0
∴y=xlnx在是减函数
故选C
点评：本题考查导函数与函数单调性的关系：导函数大于0则函数单增；导函数小于0函数单减．
分析：求出y=xlnx与y=xe-x的导函数，判断出导函数的符号，利用导函数小于0，函数单减，函数大于0，函数单增，判断出函数的单调性，利用基本初等函数的单调性判断出
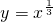与的单调性．解答：对于
∵
为R上的减函数，所以为R上的增函数对于
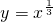是R上的增函数对于y=xe-x
∵y′=（1-x）e-x
∵
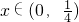
∴y′＞0
故y=xe-x在
为增函数对于y=xlnx
∵
∴
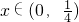
∴y′＜0
∴y=xlnx在
是减函数故选C
点评：本题考查导函数与函数单调性的关系：导函数大于0则函数单增；导函数小于0函数单减．
练习册系列答案
相关题目
（2006•静安区二模）某种洗衣机在洗涤衣服时，需经过进水、清洗、排水、脱水四个连续的过程．假设进水时水量匀速增加，清洗时水量保持不变．已知进水时间为4分钟，清洗时间为12分钟，排水时间为2分钟，脱水时间为2分钟．洗衣机中的水量y（升）与时间x（分钟）之间的关系如下表所示：