题目内容
下列命题中:①函数,f(x)=sinx+ (x∈(0,π))的最小值是2
(x∈(0,π))的最小值是2 ;②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形;③如果正实数a,b,c满足a + b>c则
;②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形;③如果正实数a,b,c满足a + b>c则 +
+ >
> ;④如果y=f(x)是可导函数,则f′(x)=0是函数y=f(x)在x=x处取到极值的必要不充分条件.其中正确的命题是( )
;④如果y=f(x)是可导函数,则f′(x)=0是函数y=f(x)在x=x处取到极值的必要不充分条件.其中正确的命题是( )A.①②③④
B.①④
C.②③④
D.②③
【答案】分析:根据基本不等式和三角函数的有界性可知真假,利用题设等式,根据和差化积公式整理求得cos(A+B)=0或sin(A-B)=0,推断出A+B= 或A=B,则三角形形状可判断出.构造函数y=
或A=B,则三角形形状可判断出.构造函数y= ,根据函数的单调性可证得结论;由函数极值点与导数的关系,我们易判断对错.
,根据函数的单调性可证得结论;由函数极值点与导数的关系,我们易判断对错.
解答:解:①f(x)=sinx+ ≥2
≥2 ,当sinx=
,当sinx= 时取等号,而sinx的最大值是1,故不正确;
时取等号,而sinx的最大值是1,故不正确;
②∵sin2A=sin2B∴sin2A-sin2B=cos(A+B)sin(A-B)=0
∴cos(A+B)=0或sin(A-B)=0∴A+B= 或A=B
或A=B
∴三角形为直角三角形或等腰三角形,故正确;
③可构造函数y= ,该函数在(0.+∞)上单调递增,a+b>c则
,该函数在(0.+∞)上单调递增,a+b>c则 +
+ >
> ,故正确;
,故正确;
④∵f(x)是定义在R上的可导函数,
当f′(x)=0时,x可能f(x)极值点,也可能不是f(x)极值点,
当x为f(x)极值点时,f′(x)=0一定成立,
故f′(x)=0是x为f(x)极值点的必要不充分条件,故④正确;
故选C.
点评:考查学生会利用基本不等式解题,注意等号成立的条件,同时考查了极值的有关问题,属于综合题.
 或A=B,则三角形形状可判断出.构造函数y=
或A=B,则三角形形状可判断出.构造函数y= ,根据函数的单调性可证得结论;由函数极值点与导数的关系,我们易判断对错.
,根据函数的单调性可证得结论;由函数极值点与导数的关系,我们易判断对错.解答:解:①f(x)=sinx+
 ≥2
≥2 ,当sinx=
,当sinx= 时取等号,而sinx的最大值是1,故不正确;
时取等号,而sinx的最大值是1,故不正确;②∵sin2A=sin2B∴sin2A-sin2B=cos(A+B)sin(A-B)=0
∴cos(A+B)=0或sin(A-B)=0∴A+B=
 或A=B
或A=B∴三角形为直角三角形或等腰三角形,故正确;
③可构造函数y=
 ,该函数在(0.+∞)上单调递增,a+b>c则
,该函数在(0.+∞)上单调递增,a+b>c则 +
+ >
> ,故正确;
,故正确;④∵f(x)是定义在R上的可导函数,
当f′(x)=0时,x可能f(x)极值点,也可能不是f(x)极值点,
当x为f(x)极值点时,f′(x)=0一定成立,
故f′(x)=0是x为f(x)极值点的必要不充分条件,故④正确;
故选C.
点评:考查学生会利用基本不等式解题,注意等号成立的条件,同时考查了极值的有关问题,属于综合题.

练习册系列答案
相关题目
下列命题中:
①函数f(x)=sinx+
(x∈(0,π))的最小值是2
;
②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形:
③如果正实数a,b,c满足a+b>c,则
+
>
;其中正确的命题是( )
①函数f(x)=sinx+
| 2 |
| sinx |
| 2 |
②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形:
③如果正实数a,b,c满足a+b>c,则
| a |
| 1+a |
| b |
| 1+b |
| c |
| 1+c |
| A、①②③ | B、① | C、②③ | D、③ |
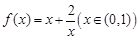 的最小值是
的最小值是 ;②对于任意实数
;②对于任意实数 ,有
,有 且
且 时,
时, ,
,
 ,则
,则 时,
时, ;③如果
;③如果 是可导函数,则
是可导函数,则 是函数
是函数 处取到极值的必要不充分条件;④已知存在实数
处取到极值的必要不充分条件;④已知存在实数 成立,则实数
成立,则实数 的取值范围是
的取值范围是 。其中正确的命题是___________.
。其中正确的命题是___________.