题目内容
下列几个命题:
①关于x的不等式ax<
在(0,1)上恒成立,则a的取值范围为(-∞,1];
②函数y=log2(-x+1)+2的图象可由y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位得到;
③若关于x方程|x2-2x-3|=m有两解,则m=0或m>4;
④若函数f(2x+1)是偶函数,则f(2x)的图象关于直线x=
对称.
其中正确的有______.
①关于x的不等式ax<
| 2x-x2 |
②函数y=log2(-x+1)+2的图象可由y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位得到;
③若关于x方程|x2-2x-3|=m有两解,则m=0或m>4;
④若函数f(2x+1)是偶函数,则f(2x)的图象关于直线x=
| 1 |
| 2 |
其中正确的有______.
关于x的不等式ax<
在(0,1)上恒成立,即a<
=
在(0,1)上恒成立,当x∈(0,1)时,
>1,故a的取值范围为(-∞,1],即①正确;
将y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位可得y=log2[-(x-2]-1)-2+4=log2(-x+1)+2的图象,故②正确;
函数y=|x2-2x-3|是将抛物线y=x2-2x-3的图象位置x轴下方的翻折到x轴上方,且在x=-1或x=3时取极小值0,当x=1时取极大值4,故当m=0或m>4时与直线y=m有两个交点,故③正确;
f(2x)的图象是由f(2x+1)的图象向右平移
个单位得到的,若函数f(2x+1)是偶函数,则其图象关于y轴对称,故f(2x)的图象关于直线x=
对称,即④正确;
故答案为:①②③④
| 2x-x2 |
| ||
| x |
|
|
将y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位可得y=log2[-(x-2]-1)-2+4=log2(-x+1)+2的图象,故②正确;
函数y=|x2-2x-3|是将抛物线y=x2-2x-3的图象位置x轴下方的翻折到x轴上方,且在x=-1或x=3时取极小值0,当x=1时取极大值4,故当m=0或m>4时与直线y=m有两个交点,故③正确;
f(2x)的图象是由f(2x+1)的图象向右平移
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:①②③④

练习册系列答案
相关题目
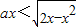 在(0,1)上恒成立,则a的取值范围为(-∞,1];
在(0,1)上恒成立,则a的取值范围为(-∞,1];  对称.
对称. 在(0,1)上恒成立,则a的取值范围为(-∞,1];
在(0,1)上恒成立,则a的取值范围为(-∞,1];  对称.
对称. 在(0,1)上恒成立,则a的取值范围为(-∞,1];
在(0,1)上恒成立,则a的取值范围为(-∞,1];  对称.
对称.