题目内容
已知数列{ }中,
}中, (t>0且t≠1).若
(t>0且t≠1).若 是函数
是函数 的一个极值点.
的一个极值点.
(Ⅰ)证明数列{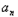 +1﹣
+1﹣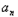 }是等比数列,并求数列{
}是等比数列,并求数列{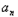 }的通项公式;
}的通项公式;
(Ⅱ)记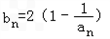 ,当t=2时,数列{bn}的前n项和为
,当t=2时,数列{bn}的前n项和为 ,求使
,求使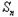 >2008的n的最小值;
>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有 .
.
 }中,
}中, (t>0且t≠1).若
(t>0且t≠1).若 是函数
是函数 的一个极值点.
的一个极值点.(Ⅰ)证明数列{
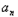 +1﹣
+1﹣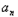 }是等比数列,并求数列{
}是等比数列,并求数列{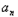 }的通项公式;
}的通项公式;(Ⅱ)记
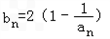 ,当t=2时,数列{bn}的前n项和为
,当t=2时,数列{bn}的前n项和为 ,求使
,求使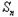 >2008的n的最小值;
>2008的n的最小值;(Ⅲ)当t=2时,求证:对于任意的正整数n,有
 .
.解:(Ⅰ)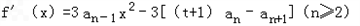 .
.
由题意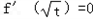 ,即
,即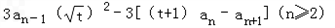 ,
,
∴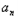 +1﹣
+1﹣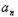 =t(
=t(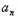 ﹣
﹣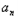 ﹣1)(n≥2),
﹣1)(n≥2),
∵t>0且t≠1,
∴数列{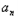 +1﹣
+1﹣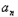 }是以t2﹣t为首项,t为公比的等比数列,
}是以t2﹣t为首项,t为公比的等比数列,
∴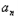 +1﹣
+1﹣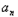 =(t2﹣t)tn﹣1=(t﹣1)tn
=(t2﹣t)tn﹣1=(t﹣1)tn
∴a2﹣a1=(t﹣1)t
a3﹣a2=(t﹣1)t2
…
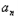 ﹣
﹣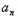 ﹣1=(t﹣1)tn﹣1
﹣1=(t﹣1)tn﹣1
以上各式两边分别相加得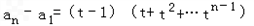 ,
,
∴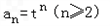 ,
,
当n=1时,上式也成立,
∴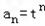
(Ⅱ)当t=2时,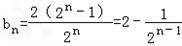
∴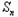 =2n﹣(1+
=2n﹣(1+ +
+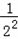 +…+
+…+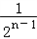 )=
)=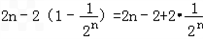 .
.
由 >2008,得
>2008,得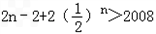 ,
, ,
,
当n≤1004时,n+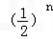 <1005,
<1005,
当n≥1005时,n+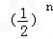 >1005,
>1005,
因此n的最小值为1005.
(Ⅲ)∵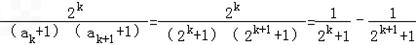
∴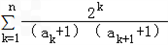 =
=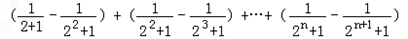
=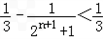
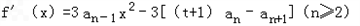 .
.由题意
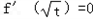 ,即
,即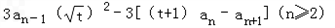 ,
,∴
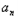 +1﹣
+1﹣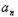 =t(
=t(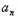 ﹣
﹣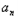 ﹣1)(n≥2),
﹣1)(n≥2),∵t>0且t≠1,
∴数列{
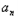 +1﹣
+1﹣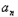 }是以t2﹣t为首项,t为公比的等比数列,
}是以t2﹣t为首项,t为公比的等比数列,∴
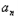 +1﹣
+1﹣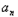 =(t2﹣t)tn﹣1=(t﹣1)tn
=(t2﹣t)tn﹣1=(t﹣1)tn∴a2﹣a1=(t﹣1)t
a3﹣a2=(t﹣1)t2
…
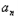 ﹣
﹣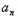 ﹣1=(t﹣1)tn﹣1
﹣1=(t﹣1)tn﹣1以上各式两边分别相加得
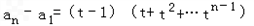 ,
,∴
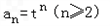 ,
,当n=1时,上式也成立,
∴
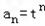
(Ⅱ)当t=2时,
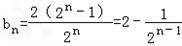
∴
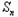 =2n﹣(1+
=2n﹣(1+ +
+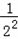 +…+
+…+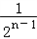 )=
)=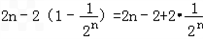 .
.由
 >2008,得
>2008,得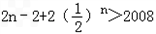 ,
, ,
,当n≤1004时,n+
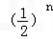 <1005,
<1005,当n≥1005时,n+
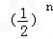 >1005,
>1005,因此n的最小值为1005.
(Ⅲ)∵
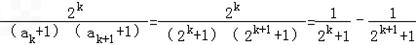
∴
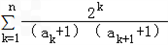 =
=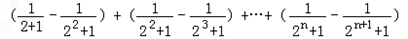
=
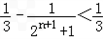

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目

 (t>0且t≠1).若
(t>0且t≠1).若 是函数
是函数 的一个极值点.
的一个极值点.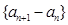 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;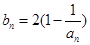 ,当t=2时,数列
,当t=2时,数列 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;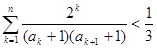 。
。