题目内容
在R上定义运算x?y=x（1-y），若不等式（-ax）?（3+x）＞-1对于任意x恒成立，则a的范围为（ ）
分析：利用新定义，不等式转化为ax2+2ax+1＞0，通过对a分类讨论，利用一元二次不等式的解法即可得出．
解答：解：由新定义可得：-ax[1-（3+x）]＞-1，化为ax2+2ax+1＞0，
①当a=0时，化为1＞0恒成立；
②当a≠0时，∵ax2+2ax+1＞0，对于任意x恒成立，∴
，解得0＜a＜1．
综上可知：a的范围为[0，1）．
故选B．
①当a=0时，化为1＞0恒成立；
②当a≠0时，∵ax2+2ax+1＞0，对于任意x恒成立，∴
|
综上可知：a的范围为[0，1）．
故选B．
点评：正确理解新定义和熟练掌握分类讨论思想方法、一元二次不等式的解法等是解题的关键．
练习册系列答案
相关题目
：
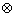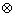×y=x(1-y).若不等式(x-a)
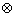(x+a)＜1对任意实数x成立，则( ) 
＜a＜
D.
＜a＜