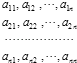题目内容
【题目】数列{an}中,已知a1= ![]() ,an+1=
,an+1= ![]() .
.
(1)证明:an<an+1< ![]() ;
;
(2)证明:当n≥2时,( ![]() )
) ![]() <2.
<2.
【答案】
(1)证明:由 ![]() ,得
,得 ![]() ,即0≤an≤1.
,即0≤an≤1.
∴an+1= ![]() =
= ![]() ,
,
又a1= ![]() ≠0,且
≠0,且 ![]() ,∴0
,∴0 ![]() .
.
∴ ![]() >0.
>0.
即 ![]()
(2)证明:当n=2时, ![]() ,
,
又∵ ![]() ,
,
∴ ![]() .
.
即当n=2时, ![]() 成立,
成立,
当n=k时, ![]() 成立,即
成立,即 ![]() 成立,
成立,
当n=k+1时, ![]() =
= ![]() .
.
∵an+1>an,∴ak+1>ak
∴ ![]() .
.
则 ![]() =
= ![]() ,
,
∴当n=k+1时, ![]() 也成立,
也成立,
∴当n≥2时, ![]() 成立
成立
【解析】(1)由已知a1= ![]() ,an+1=
,an+1= ![]() ,即可得到
,即可得到 ![]() ,又0
,又0 ![]() ,进一步得到
,进一步得到 ![]() ,则结论an<an+1<
,则结论an<an+1< ![]() 可证;(2)首先证当n=2时,
可证;(2)首先证当n=2时, ![]() 成立,即当n=k时,
成立,即当n=k时, ![]() 成立,当n=k+1时,ak+1>ak , 则
成立,当n=k+1时,ak+1>ak , 则 ![]() =
= ![]() ,则结论当n≥2时,(
,则结论当n≥2时,( ![]() )
) ![]() <2可证.
<2可证.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.

【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合 计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合 计 | 60 | 50 | 110 |
根据上述数据能得出的结论是( )
(参考公式与数据:X2= ![]() .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
.当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
A.有99%的把握认为“爱好该项运动与性别有关”
B.有99%的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.