Question

某班共50人报名参加两项比赛，参加A项共有30人，参加B项共有33人，且A，B两项都不参加的人数比A，B都参加的人数的

1

3

多1人，则只参加A项不参加B项的有

9

人．

Answer 1

分析：利用Venn图，将满足条件的集合人数确定即可．

解答：解：设A，B都参加的人数为x，则A，B两项都不参加的人数为

1

3

x+1，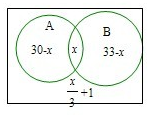
则只参加A的有30-x人，只参加B的有33-x人．
则满足30-x+x+33-x+

1

3

x+1=50．
即64-

2

3

x=50，
解得x=21．
所以只参加A项不参加B项的有30-21=9．
故答案为：9．

点评：本题主要考查集合元素个数的确定，利用Venn图，建立方程关系是解决此类问题的基本方法．