题目内容
已知函数f(x)=loga[ -(2a)x]对任意x∈[
-(2a)x]对任意x∈[ ,+∞)都有意义,则实数a的取值范围是
,+∞)都有意义,则实数a的取值范围是
- A.(0,
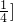
- B.(0,
 )
) - C.[
 ,1)
,1) - D.(
 ,
, )
)
B
分析:由题意知,x∈[ ,+∞)时,对数的真数[
,+∞)时,对数的真数[ -(2a)x]>0恒成立,当x=
-(2a)x]>0恒成立,当x= 时,真数大于0也成立,解不等式
时,真数大于0也成立,解不等式
求出实数a的取值范围.
解答:当x= 时,对数的真数[
时,对数的真数[ -(2a)x]=
-(2a)x]= -
- >0成立,∴
>0成立,∴ >
> ,
,
 >2a>0,∴0<a<
>2a>0,∴0<a< ,
,
故选 B.
点评:本题考查对数函数的定义域,以及不等式的解法.
分析:由题意知,x∈[
 ,+∞)时,对数的真数[
,+∞)时,对数的真数[ -(2a)x]>0恒成立,当x=
-(2a)x]>0恒成立,当x= 时,真数大于0也成立,解不等式
时,真数大于0也成立,解不等式求出实数a的取值范围.
解答:当x=
 时,对数的真数[
时,对数的真数[ -(2a)x]=
-(2a)x]= -
- >0成立,∴
>0成立,∴ >
> ,
, >2a>0,∴0<a<
>2a>0,∴0<a< ,
,故选 B.
点评:本题考查对数函数的定义域,以及不等式的解法.

练习册系列答案
相关题目