题目内容
在一幢10米高的楼顶测得对面一塔吊顶的仰角为60°,塔基的俯角为45°,那么这座塔吊的高是( )
分析:设楼高AB=10米,塔高为CE,则∠DAE=60°,∠DAC=45°,CD=AB,在直角三角形ADE中可求得DE,从而可得出塔吊的高度.
解答:解:由题意,设楼高AB=10米,塔高为CE
∵测得对面一塔吊顶的仰角为60°,塔基的俯角为45°
∴∠DAE=60°,∠DAC=45°,∴ABCD是正方形,
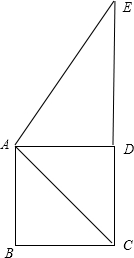
∴CD=AB=10米
再由∠DAE=60°,在直角三角形ADE中可求得DE=ADtan60°=10
米
∴塔高为DE+CD=10+10
=10(1+
)米
故选B.
∵测得对面一塔吊顶的仰角为60°,塔基的俯角为45°
∴∠DAE=60°,∠DAC=45°,∴ABCD是正方形,

∴CD=AB=10米
再由∠DAE=60°,在直角三角形ADE中可求得DE=ADtan60°=10
| 3 |
∴塔高为DE+CD=10+10
| 3 |
| 3 |
故选B.
点评:解三角形的应用一般是求距离(长度问题,高度问题等)解题时要注意综合利用所学的知识与题设中的条件,求解三角形的边与角.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 ,塔基的俯角为
,塔基的俯角为 ,那么这座塔吊的高是( )
,那么这座塔吊的高是( )  B.
B. C.
C. D.
D.
 ,塔基的俯角为
,塔基的俯角为 ,那么这座塔吊的高是 .
,那么这座塔吊的高是 .