题目内容
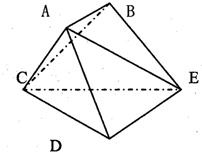 如图,多面体ABCDE中,AB⊥面ACD,DE⊥面ACD;三角形ACD是正三角形,且AD=DE=2,AB=1
如图,多面体ABCDE中,AB⊥面ACD,DE⊥面ACD;三角形ACD是正三角形,且AD=DE=2,AB=1(1)求直线AE和面CDE所成角的正切值;
(2)求多面体ABCDE的体积;
(3)判断直线CB和AE能否垂直,证明你的结论.
分析:(1)由题意及所给图形,要求线面角,必需找到该斜线与其射影的夹角,而射影线是斜足与垂足所成的线,进而在三角形中求出线面角 即可;
(2)利用棱锥的体积公式,由平面ABED⊥平面ACD,利用两垂直平面的性质的到线面垂直,进而求出四棱锥的体积;
(3)利用向量的知识,利用线面垂直的判定定理证出线面垂直,进而得到线线垂直.
(2)利用棱锥的体积公式,由平面ABED⊥平面ACD,利用两垂直平面的性质的到线面垂直,进而求出四棱锥的体积;
(3)利用向量的知识,利用线面垂直的判定定理证出线面垂直,进而得到线线垂直.
解答: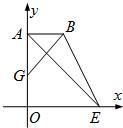 解:(1)取CD的中点F,连接AF、EF,△ACD为正三角形,
解:(1)取CD的中点F,连接AF、EF,△ACD为正三角形,
∴AF⊥CD,DE⊥平面ACD,
∴平面CDE⊥平面ACD,
∴AF⊥平面CDE,∠AEF为所求AE和平面CDE所成的角,AF=
,EF=
,tan∠AEF=
直线AE和面CDE所角的正切值是
.
(2)取AD中点G,平面ABED⊥平面ACD,CG⊥AD,
∴CG⊥平面ABED
∴V=
SABED•CG=
×
×
=
(3)证明:CB⊥AE,如图建立坐标系:
则E(2,0),A(0,2),B(1,2),G(0,1),
=(2,-2),
=(1,1),
•
=0,
∴AE⊥GB
∵CG⊥AE,11
∴AE⊥平面CGB,∴AE⊥CB.
 解:(1)取CD的中点F,连接AF、EF,△ACD为正三角形,
解:(1)取CD的中点F,连接AF、EF,△ACD为正三角形,∴AF⊥CD,DE⊥平面ACD,
∴平面CDE⊥平面ACD,
∴AF⊥平面CDE,∠AEF为所求AE和平面CDE所成的角,AF=
| 3 |
| 5 |
| ||
| 5 |
直线AE和面CDE所角的正切值是
| ||
| 5 |
(2)取AD中点G,平面ABED⊥平面ACD,CG⊥AD,
∴CG⊥平面ABED
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1+2 |
| 2 |
| 3 |
| 3 |
(3)证明:CB⊥AE,如图建立坐标系:
则E(2,0),A(0,2),B(1,2),G(0,1),
| AE |
| GB |
| AE |
| GB |
∴AE⊥GB
∵CG⊥AE,11
∴AE⊥平面CGB,∴AE⊥CB.
点评:(1)此问重点考查了利用面面垂直的性质得到线面垂直,还考查了线面角的概念及线面角的求法;
(2)此问重点考查了四棱锥的体积公式;
(3)此问重点考查了利用向量的知识求证线面垂直进而得到线面垂直.
(2)此问重点考查了四棱锥的体积公式;
(3)此问重点考查了利用向量的知识求证线面垂直进而得到线面垂直.

练习册系列答案
相关题目


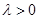 使得
使得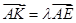 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为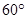 ,求
,求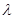 的值。
的值。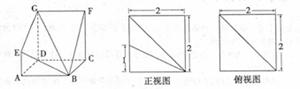
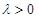 使得
使得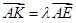 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为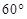 ,求
,求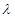 的值。
的值。
 使得
使得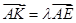 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为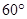 ,求
,求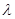 的值。
的值。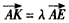 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。